�Ŀ���07���������⡡��§��������
�Ŀ���2007ǯ�١���������ꡡ��5�䡡�Ǥ���
��§��������Ǥ���
����ʸ��Ĺ���Τǡ����ä�������褦���ɤߤޤ���
(1)��(2)�����̤˲ޤ���
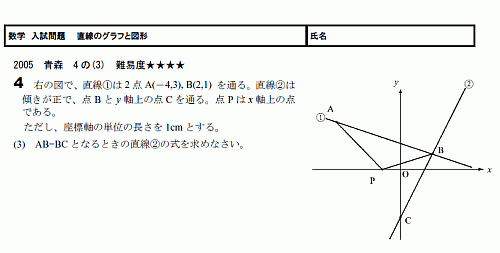
(3)���������Ǥ���
(3)�Τ߲��⡣
���ҥ��
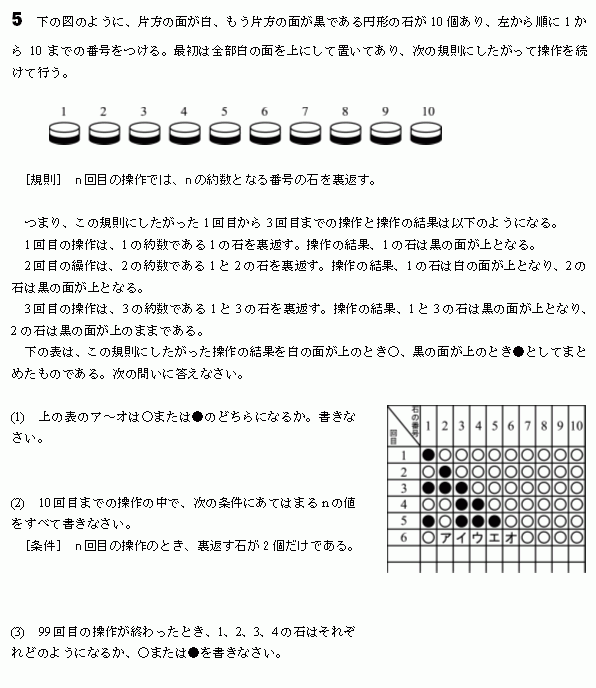
�ֲ��Ĥ��ġ��¤�Ǥ��뤫�ͤ��ޤ���
������
1���ܤ��Ф�2��1��(����)��³���Ƥ��ޤ���
2���ܤ��Ф�4��1��(��������)
3���ܤ��Ф�6�Ĥ�1��(������������)
4���ܤ��Ф�8��1��(����������������)
�����줾���¤�Ǥ������Ȥ�ʬ����ޤ���
1���ܤ��Ф�99��2��49���ޤ�1���������
(2�Ĥ��Ĥ��Ȥ�49�Ȥ��ä�1��;�롣)
2���ܤ��Ф�99��4��24���ޤ�3�����顢����
(4�Ĥ��Ĥ��Ȥ�24�Ȥ��ä�3��;�롣)
3���ܤ��Ф�99��6��16���ޤ�3���������
(6�Ĥ��Ĥ��Ȥ�16�Ȥ��ä�3��;�롣)
4���ܤ��Ф�99��8��12���ޤ�3���������
(8�Ĥ��Ĥ��Ȥ�12�Ȥߤ��ä�3��;�롣)
�Ŀ�����2007ǯ�� ��������ꡡ������Ϥ�����
�Ŀ���07���������⡡��ʪ���ȿ�
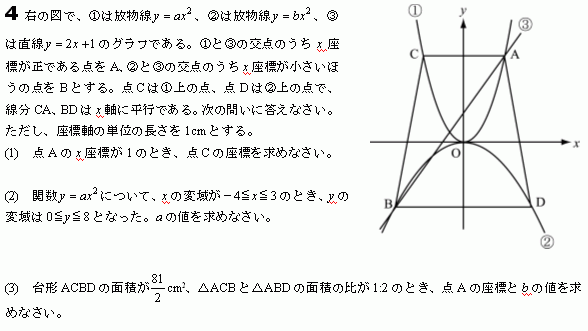
�Ŀ���2007ǯ�١���������ꡡ��4�䡡�Ǥ���
(3)������Ψ�Ϥʤ��A�κ�ɸ��2.9��b���ͤ�1.7��
�����������Ψ���㤤�ȡ��������֤ǤϼΤƤƤ⤤���Ǥ��͡�
��������˻��֤����ꡢ¾�������ߤʤ����˻��֤�Ȥä��ۤ���
ͭ���Ǥ��礦��
�����������ְʳ��ǤϤɤ���äƲΤ����ΤäƤ����Τ����Ω���ޤ���
���������ͤ��Ƥߤ褦��Ǻ����ͤϤ���ޤ���
���ҥ��
A��x��ɸ�� t �Ȥ����ơ����������äƤ����ޤ���
t��k�Ǥ⤤������p�Ǥ⤤���Ǥ���
���ѿ��ȸƤФ�Ƥ��ޤ���
������
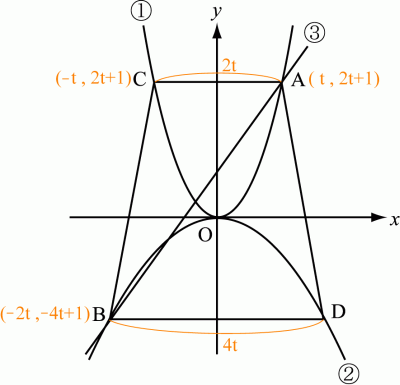
A��x��ɸ��t�Ȥ���ȡ�A��y��2x+1����������顢
y��2t��1��
��äơ�A(t , 2t��1)��
A��C��y���ˤĤ��ơ��оΤ��������顢
C(-t , 2t��1)��
��äơ�
AC��2t��
��ACB�Ȣ�ABD�����Ѥ��椬1��2��
������Ĥλ��ѷ���AC��BD�줾������դ��ȹͤ���ȡ�
�⤵����������
�Ĥޤꡢ���դ��椬1��2�Ȥʤ롣
�����顢AC��BD��1��2��
AC��2t�����顢BD��4t��
BD��4t�Ȥ������Ȥϡ�B��x��ɸ��4t��Ⱦʬ��2t�˥ޥ��ʥ���Ĥ�����ΤȤʤ롣
�Ĥޤꡢ-2t��
B�� y��2x��1����������顢x��ɸ��-2t�����������y��-4t��1��
��ä�B(-2t , -4t��1)��
����ȡ�����ι⤵��2t��1��(��4t��1)��6t��
��äơ����Ѥ�81/2�Ǥ��뤳�Ȥ��Ȥ�t����������Ĥ���ȡ�
(2t��4t)��6t��2��81/2
�����ȡ�t���3/2��
A��x��ɸ�ϥץ饹�����顢3/2��
A( 3/2 , 4 )
��������b���ͤ���ޤ���
t��3/2�ʤΤǡ�B(-2t , -4t��1)����������ȡ�
B( -3 , -5)��
�����y��bx^2�μ����������ơ�
b=-5/9
�Ŀ�����2007ǯ�� ��������ꡡ������Ϥ�����
�Ŀ���07���������⡡����������
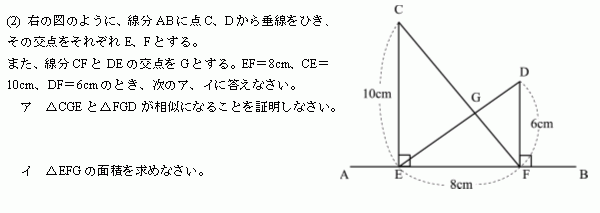
�Ŀ���2007ǯ�١���������ꡡ��3�䡡(2)�Ǥ���
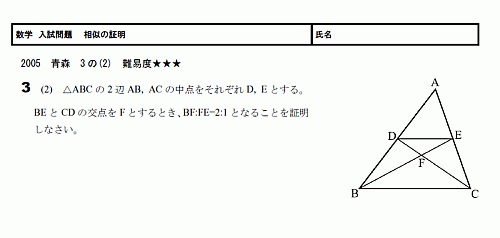
����ξ���������θ�ǡ��������ȤäƲ����ꡣ
��������Ψ��15��������Ǥ���
���ʻҤ�¿���Ǥ���
��������������⡣
���ҥ��
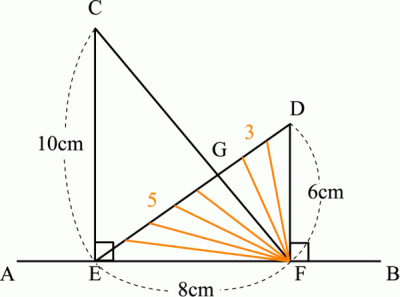
����ʻ��ѷ������Ȥä����Ѥ���ޤ���
������
����ꡢ��CGE�Ȣ�FGD�������
������CE��FD��10��6��5��3
��äơ�EG��DG��5��3��������
��DEF�����Ѥ�8��6��1/2��24
����ꡢ��EFG�����ѤϢ�DEF��8ʬ��5��
��äơ���EFG��24��5/8��15cm^2
�Ȥ����ǡ�
5/8��(8ʬ��5��)�ΤȤ���������Ǥ��ʤ����̤�����¿���Ǥ���
ʬ���Ǹ�����ȡ���̣��ʬ����ʤ��ΤǤ���
8ʬ��5�ϡ�8�Ĥ�������ʬ����������5��ʬ�פȤ�����̣�Ǥ���
����ޤ�ܤ�������Ǥ��ޤ���
�ʲ��οޤͤˤ��ơ���EFG����DEF��8�Ĥ�������ʬ����������5��ʬ�פǤ��뤳�Ȥ�
�Τˤ��ߤ��ޤ����ߤ����Ǥ���
�Ŀ�����2007ǯ�� ��������ꡡ������Ϥ�����
�Ŀ���07���������⡡���Ѥ��濴��

�Ŀ���2007ǯ�١���������ꡡ��1�䡡(6)�Ǥ���
����Ψ��36��������Ǥ���
����⤽��ۤ�������ǤϤʤ��ΤǤ�����������
�ʤ�Ǥ���������Ψ���㤯�ʤ�ΤǤ��礦����
�Ŀ�Ū�ˤ�60���ޤǤϤ����Ȼפ��ΤǤ�����������
���ҥ��
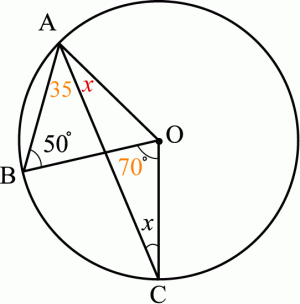
�����ջ��ѷ�����Ѥ���������
�������̤��濴�Ѥϱ��Ѥ�2�ܡ�
������
��BOC��70�٤ʤΤǡ���BC�α��ѤǤ����BAC�Ϥ���Ⱦʬ��35�١�
��OAC�Ȣ�OBA�������ջ��ѷ�(Ʊ���ߤ�Ⱦ�¤�����������)��
��äƢ�OAC��x����OAB��50�١�
x��50��35��15�١�
��������Ǥ����顢������ޤ���Ƭ��������ǽ�������褦�ˤ���ȡ�
���μ�����꤬���դˤʤ�褦�ʵ������ޤ���
��������Ϥ�������ľ���Ϥ�ɬ�פǤ���
�������������������㤴���㤷�Ƥ���ȡ�
ľ���Ϥ��ܤ��ʤ��ΤǤϤʤ����ȻפäƤ��ޤ���
�����顢�����������顢�ޤ�����ǽ����Ǥ���褦���ä��ޤ���
����Ż�����褦�ʴ����Ǥ���
�Ŀ�����2007ǯ�� ��������ꡡ������Ϥ�����
�Ŀ���07���������⡡ʿ�����η�

�Ŀ���2007ǯ�١���������ꡡ��1�䡡(5)�Ǥ���
����Ψ��36��������Ǥ���
��ä����Ȥʤ��������������Ψ��������ΤǤ��礦��
����ۤ�������ǤϤ���ޤ���
���ҥ��
��27��������ñ�ˤ��ƹͤ��ޤ���
������
�롼�Ȥ�����ñ�ˤ��Ƥߤޤ���
��3�ܢ�a��3��3
�ɤ�������̣����ͤ��ơ����Ф餯į��ޤ���
�֢�3��ʤˤ�����3��3������������
��������Ȣ�a��2��3���ȼ�������Ω�Ĥ��Ȥ˵����Ĥ��ޤ���
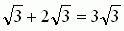
��a��2��3���������a���12
��äơ�a��12
�Ŀ�����2007ǯ�� ��������ꡡ������Ϥ�����
�̳�ƻ07�����⡡��ʿ�������� Ω��

�̳�ƻ2007ǯ�ٹ�����������5�����3�Ǥ���
����Ψ��0.4%���㤤�Ǥ��͡�
Ω�Τ����������Ψ���㤯�ʤ�ޤ�����������㤹���ޤ��͡�
���ҥ��
Ω�Τޤ�ʬ�䤷�ƹͤ��ޤ���
������
ʬ�䤹��Ȱʲ��Τ褦�ˤʤ�ޤ���
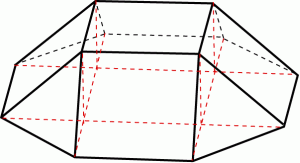
(������Ȥ��Ƥϡ���Ʀ�塣������夫��4�����줿�����Ǥ���)
3�����Ω�Τ�9�Ľ���ޤ���
������λͳ�������Ѥ�
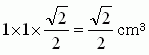
4�ĤǤ��뻰�ѿ��ϤҤȤĤˤޤȤ��ȡ��ͳѤ����ˤʤ�ޤ���
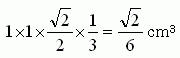
�Ĥä���������Ȥߤ��碌���1�Ĥλͳ��줬�Ǥ��ޤ���
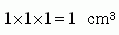
���٤Ƥ��碌��ȡ�
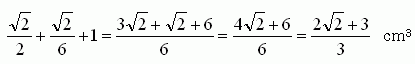
�̳�ƻ07�����⡡��ʿ��������

�̳�ƻ2007ǯ�ٹ�����������5�����2�Ǥ���
����Ψ��7.8%���㤤�Ǥ��͡�
�ͤ�����ʣ������ޤ���������ʣ���ˤʤäƤ��ޤ��ȤĤ餤�Ȥ����Ǥ���
�ʤ�٤�����ץ�ʹͤ����ɵ᤹�٤��Ǥ���
(���֤��¤��Ƥ���Τ�����������Ȼפ��ޤ�����)
���ҥ��
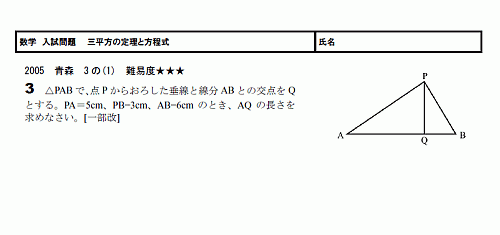
Ŭ�ڤ�������������뤳�ȤǤ���
CF�α�Ĺ��A�ȸ��ꡢ��ABC��ľ�������ջ��ѷ��Ȥʤ�ޤ���
��AHF��ľ�������ջ��ѷ��Ȥʤ�ޤ���
������
2�ܤ������������Ȳ��Τ褦�ʿޤˤʤ�ޤ���
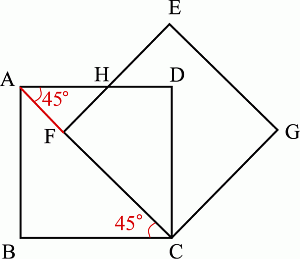
��ABC��ľ�������ջ��ѷ������顢AC��5��2cm��
FC��5cm�����顢AF��5��2��5cm��
��AHF��ľ�������ջ��ѷ������顢AH��AF�ߢ�2��(5��2��5)�ߢ�2��10��5��2��
AH��10��5��2cm��
�̳�ƻ07�����⡡2���ؿ��Υ����
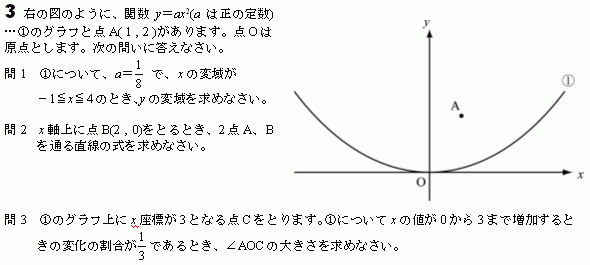
�̳�ƻ2007ǯ�ٹ�����������3��Ǥ���
��3������٤��⤤(����Ψ19%)�Τǡ������
���ҥ��
�ޤ�������ʪ����a���ͤ���ޤ���
������C�κ�ɸ����ޤ���
��AOC���ɤ�ʻ��ѷ���Ĵ�٤ޤ���
���٤�Ϳ�����Ƥ��ʤ��Τˡ�
�ֳ��٤���ʤ����פȤ����Ƥ��ޤ���
�Ȥ������Ȥϡ��ɤ����������ѷ��仰���구�λ��ѷ��ʤ�
���̤ʷ�������Ϥ��Ǥ���
������
C�κ�ɸ��(3,1)�Ȥʤ�ޤ���
�����ʳ��ǡ����Τ褦�ʿޤ��⤫��Ǥ�����ɤ��Ǥ���
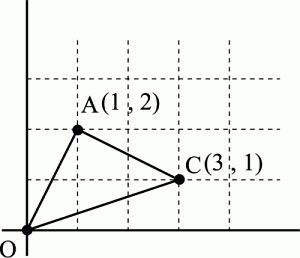
(�ޤ����ۤȤ�ɤ����̤ˤ��⤫��Ǥ��ޤ���)
��οޤơ�
OA��AC�ǡ���OAC��90�������
ľ�������ջ��ѷ����ʡ��ȵ����Ĥ���Ф����ΤǤ�����
��������ѤǤ���
¾�ˤ�OA��AC��OC��Ĺ����ʿ���������ˤ�äƵ��ơ�
��Ӥ��ƤߤƤ⤤���Ǥ���
ľ�������ջ��ѷ��Ǥ��뤳�Ȥ˵����Ĥ��ޤ���
������ˤ��衢�����̤ʷ��Ǥ���Ϥ����פȸ�����Ĥ��ơ�
����į��뤳�Ȥ�ɬ�פǤ���
�̳�ƻ07�����⡡������������

�̳�ƻ2007ǯ�ٹ�����������2�䡢��1�Ǥ���
������21��
���ҥ��
A�λ��ߤ�£�볨�Ϥ����ο��Ǽ����ġ�
B�λ��ߤ�£�볨�Ϥ����ο��Ǽ����ĺ�ꡢ
��Ĥ�����Ƿ�٤�褦��Ĵ�����ޤ���
������
����������3ʬ��1�פȤ������Ȥ�¾��������3ʬ��2�ˤʤ�ޤ���
�ޤ������������Τ���10�͡פ��Ф���ۤ��������ϡ�x��10(��)�פȤʤ�ޤ���
���������դ��Ƽ���Ω�Ƥ�ȡ�
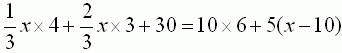
�Ȥʤ�ޤ���
������12�͡�
�̳�ƻ07�����⡡��ʿ�������� ����Ϣ������

�̳�ƻ2007ǯ�ٹ�����������1�䡢��7�Ǥ���
Ŭ�ڤ��������������Ф���ۤ�������ǤϤ���ޤ���
����Ψ���㤯��18.7��������Ǥ���
���ҥ��
��ϻ�ѷ���1�ĤγѤ�120�١�
��ʿ����������
����Ϣ��������
������
A��C���Ӥޤ���
B������ʬAC�˿������������ä��Ȥ�����H�Ȥ��ޤ���
��BAH����Ѥ�30�١�60�١�90�٤����̤ʻ��ѷ��ʤΤǡ�
1:2:��3���椬�Ȥ��ޤ���
��äơ�AH��2��3cm��AC��AH��2�ܤ�����4��3cm��
PQ�Ϣ�ABC������Ϣ�������ˤ�äƵ����ޤ���
PQ��AC��Ĺ����Ⱦʬ������2��3cm��
�Ŀ�������������ꡡ���� 07
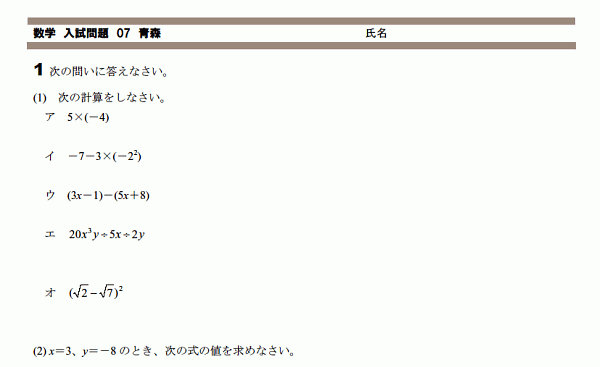
�Ŀ�����2007ǯ�٤�����Ϻ�ǯ�٤��������٤ơ������䤵�����ʤä����ݤǤ���
���Υ�٥�Ǥ���ж��ʽ�ä���ؽ����Ƥ��������������ޤ���
��Ϥꡢ4,5������Ǻ����Ĥ��Ǥ��礦��
4��(3)��������������ƹͤ��ʤ�������ˤ��ɤ��失�ޤ���
5�ε�§������������ä��Ǥ���
���������դ���ˡ§������ΤǤ��ͤ���
�츫���꤬ʣ���Ǥ���������夤������ʸ������Ǥ����(1)��(2)�����̤˲ޤ���
(3)�Ϥ���äȤ�ä����Ǥ��͡�
�Ŀ��� ��������ꡡ���� 2007ǯ��(PDF)
������ϲ�����Ѱդ��ޤ�����
���������Ф����Ѥ���������
�Ŀ�������������ꡡ���⡡��1��(5)��ʿ����
�Ŀ�������������ꡡ���⡡��1��(6)������
�Ŀ�������������ꡡ���⡡��3�䡡����������
�Ŀ�������������ꡡ���⡡��4�䡡��ʪ���ȿ�
�Ŀ�������������ꡡ���⡡��6�䡡��§��������
�̳�ƻ����������ꡡ���� 07
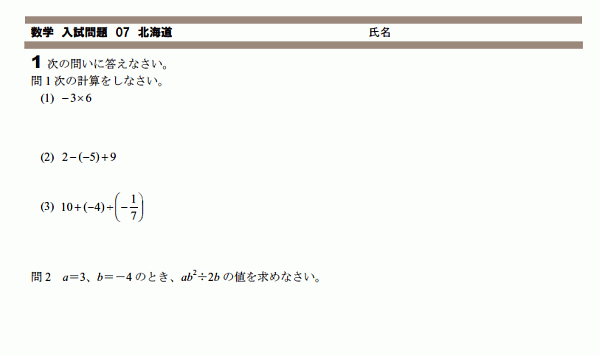
�̳�ƻ����������Ū�פ���������٤ΥХ���ɤ��Ǥ���
3����3������ϡ�����äȤ�ä����Ǥ���
���٤��ҤȤĤ⼨����Ƥ��ʤ��Τˡ����٤�����Ȥ�������Ǥ����顢
90�٤�60�٤�45�٤�30�٤��ʡ���ͽ�ۤǤ���гڤˤʤ�ޤ���
�̳�ƻ ��������ꡡ���� 2007ǯ��(PDF)
�ɵ���
������ˤĤ��Ƥϲ����ޤ�����
���ͤˤ��Ƥ���������й����Ǥ���
Ļ�踩����������ꡡ���� 06

2006ǯ��Ļ�踩������ϤȤƤ����ä��Ǥ���
�����50ʬ�DzΤ����ѤǤ���
ʿ�����Ϥ�Τ������㤤�Ϥ��Ǥ���
��������餹���ҤϤ���Τ���������
���������ޤ��ͤ��äȡ�
�����Ǥϡ��ܾ븩�����θ�������˼�������Ǥ���
Ļ�踩������Ϥ��줫�����դ��Ƹ��褦��
��ޤ�6�����꤬���⤷�����ä��Ǥ���
Ļ�踩 ��������ꡡ���� 2006ǯ��(PDF)
�²λ�������������ꡡ���� 06

2006ǯ���²λ����������ʣ�������˸����ơ��¤Ϥ䤵�������ꡢ�Ȥ������ݤǤ���
�ä�����Ϥ���ޤ���Ǥ�����
3�ε�§��������ϡ��ɤ��ٶ��ˤʤ�ΤǤϤʤ����Ȼפ��ޤ���
��§��������ιͤ�������Ȥ��ơ����ȤǻȤ������ʡ��Ȼפ��ޤ�����
�²λ��� ��������ꡡ���� 2006ǯ��(PDF)
���ɸ�����������ꡡ���� 06
���ɸ�����������ꡡ���� 06

2006ǯ�����ɸ�������Ϥ��⤷�������꤬¿���ä��Ǥ���
������������ä�����˷����Ƥ��ơ�ʿ�������㤯���ΤǤϤʤ�����ͽ�ۤ��ޤ���
�Ŀ�Ū�ˤ�4��5�����꤬���⤷�����ä��Ǥ���
�ʤ�ۤɤͤ����Ȼפ��ޤ�����
���ɸ� ��������ꡡ���� 2006ǯ��(PDF)
ʼ�˸�����������ꡡ���� 06

2006ǯ��ʼ�˸�������ϸ���Ū�ʴ��������ޤ�����
4�γ�Ψ������ΰտޤ�ʬ����ޤ���(���ݤ���������?)��
5�Ϥ錄���ι��ߤ�����Ǥ���
����դ��ɤ�����ꡣ
7��B����������ˤ��ޤ�ʤ������פǡ��Ƥ��Ƥ��⤷�����Ǥ���
ʼ�˸� ��������ꡡ���� 2006ǯ��(PDF)
�����ܡ���������ꡡ���� 06

2006ǯ�ε����ܤ�����Ϥ���������ʤ����Ȼפ��ޤ�����
���ܤη����꤬���ʤ��Τǡ����ؤ��������̤ˤȤäƤϸ�����������ä��Ȼפ��ޤ�����
Ĺ�������������Ʊ�͡��������꤬¿���ä��Ǥ���
�錄�����ͤ��뤤������Ȥϡ�
������ʣ���ˤʤꤹ���ʤ�����
��(�ѥ���������ƤϤ�륿���פ�����Ǥʤ�)����äȹͤ���ɬ�פ���������
�Ǥ��������Ԥ������¿���Ϥޤ��ˤ���Ǥ�����
����ϡ��Τμ��ȤǤ������Х�ˤ��ƻȤ���Ȼפ��ޤ���
���������Ĵ�٤Ƥߤޤ���
ʿ��18ǯ�� ��Ω���������Ȳ����˵����ܤ����꤬�ΤäƤ��ޤ���
���������
�����ܡ����츩��Ω���������Ȳ�����ʿ��18ǯ��ʿ��17ǯ��ʿ��16ǯ��ʿ��15ǯ��ʿ��14ǯ��ʿ��13ǯ��ʿ��12ǯ
�ˤ���褦�Ǥ���
������ ��������ꡡ���� 2006ǯ��(PDF)
���츩����������ꡡ���� 06

2006ǯ�μ��츩������ϤҤͤ�Τ��������꤬¿���ä��Ǥ��͡�
����������ʤ��Τǡ���İ�Ĥ��������ǫ���ɤ�ǡ���������ϳμ¤˲����Ǥ���
�Ҥͤ�Τ���������ϸ�������Ǥ��礦��
�Ŀ�Ū�ˤϼ��츩������Ϲ��ߤǤ���
���Ȼפä������1��(5)��2�λ��פ����ꡣ
���츩 ��������ꡡ���� 2006ǯ��(PDF)
���Ÿ�����������ꡡ���� 06

2006ǯ�λ��Ÿ�������ϴ���Ū�����꤬¿�����ꤵ��Ƥ��ޤ�����
����ʤ顢���ؤ��������̤⡢��ĥ�ä����������ˤʤ�ޤ���
(�����ˤ���ޤ�����)
�����4�˸Ŀ�Ū�ˤҤä�����ޤ�����
����ʬ���ƹͤ���Τ��ɤ������ݤ������ơ�
���餤�餷�Ƥ��Ƥ��ޤ��ޤ���
��Ψ������ϡ�®�����Ȥ����ˡ�
���äפ���֤�ȤäƤ��ä���ͤ���Τ�
�����Ǥ��͡�
���Ÿ� ��������ꡡ���� 2006ǯ��(PDF)
���θ� B���롼��������ꡡ���� 06

2006ǯ�ΰ��θ�B���롼�פ�����⡢A���롼�פ�������Ʊ�ͤˤҤ꤬ͤ�����Ƥ��ޤ���
B���롼�פ�����Τۤ��������꤬¿���ä��Ǥ���
���Τ֤䤵��������������Ƥ��ޤ�����
3��(5)�������1���ֹͤ����������֥��åפ��ޤ�����
�����ơ�������ʬ����ޤ�������
����ʲ����Ǥ����Τ���
�⤦����ä�������Ǥ�ʬ���륷��ץ�ʤ��äȶä���ˡ������褦�ʵ�������ΤǤ�����
�פ��Ĥ��ޤ���
ï�������Ƥ���������
(�������Ȥ��ΤϤʤ��͡�)
���θ� ��������ꡡ���� 2006ǯ��(PDF)
�������ˤ����꤬����ޤ������θ��θ��������ȤǤ���
���θ� A���롼��������ꡡ���� 06

2006ǯ�ΰ��θ�A���롼�פ�����ϡ���ľ������⤤���Ĥ�����ޤ�����
�Ҥͤ�Τ��������꤬¿���Ǥ��͡�
��������ˡ֤Ҥ��פ�ɬ�פǤ���
������ʬ����ȡ����Ϥ���(�⤦�Ϥ�äƤʤ����ˡ֥��ϡ��θ��פ���äƤ��ޤ���
���ؤ����դʥ��饹�ʤɤǡ�
1��1���Х�ˤ��ơ�
�������ζ����������Ǥ���
ȿ�Фˡ����ؤ��������̤ˤȤäƤϤ��������Ǥ��͡�
���ܤη��ä����뤳�Ȥ������Ȥ��ơ�
���̤ˤȤäơ֤Ҥ��פȤ������Ȥ����줷���θ��Ȥˤʤ�褦�ˡ�
��Ƴ�ι��פ�ɬ�פ��Ȼפ��ޤ���
���θ� ��������ꡡ���� 2006ǯ��(PDF)
�������ˤ����꤬����ޤ������θ��θ��������ȤǤ���
�Ų��� ��������ꡡ���� 06

2006ǯ���Ų���������ϡ�����������٤ι⤤����Ȥ����ΤϤ���ޤ���Ǥ�����
��������ϢΩ���������ؿ������ꡢ��������ʤɡ�
���Ҥ��ʤ���Фʤ�ʤ�����˻��֤������Ǥ���
������ʬ�ä��ꤷ�����Ǥ���
���ؤ����ʻҤˤȤäƤϡ��Ų������������𤫤⤷��ޤ���͡�
�������Ф��Ƥ���ФǤ�������Ͼ��ʤ��Ǥ����顣
�ͤ���������褦���ٶ��ˤ���٤��Ǥ���
�Ų��� ��������ꡡ���� 2006ǯ��(PDF)
���츩 ��������ꡡ���� 06

2006ǯ�δ��츩������ϡ�����Ū�����������٤��餹��ȡ�
�䤵��������ľ�����꤬¿���ä��Ȼפ��ޤ���
���Τ���ꡢ�����꤬���ʤ��Ǥ��͡�
����ñ���⤢�����٤Υ�٥�ޤǽ��Ϥ��Ƥ���ɬ�פ�����ޤ���
���츩 ��������ꡡ���� 2006ǯ��(PDF)
�����,����,���츩,���,�����,����,�ؽ�
Ĺ� ��������ꡡ���� 06

2006ǯ��Ĺ�������ϡ���ǯ�Τ��Ȥʤ��顢���˥�ˡ��������꤬¿�����ꤵ��Ƥ��ޤ�����
��������Υѥ�����Ȥ����ΤϤ���������ޤäƤ����ΤǤ�����
Ĺ�������ϤҤȤҤͤ�ä��Ƥ��ޤ���
�Ѥäȸ��Ʋ�ˡ�Υ����ǥ����������⤫�����ޤ���
�����������������Ȥ�����ʬ���ä��Ȥ���
�����Ȥ��줷�����ޤ���
���Ȥ��äơ�����ʣ���ˤʤä��ꤷ�ʤ��Ȥ����⤹�Ф餷���Ȼפ��ޤ���
�Ȥ��ˡ����������ѥ�������Τ�Ԥ������ιֻդγ������ڤ��ޤ��Ƥ����ΤǤϤʤ��Ǥ��礦����
���̤�Ĺ�������б�����ˤϡ���ˡ�ŵ������ٶ��ǤϤʤ���
�����ٶ���٤����Ȼפ��ޤ���
�������ʳ��ǡ����ä�����֤��ơ�������ͤ��Ƥߤ뤳�ȡ�
���줬������Ȼפ��ޤ���
Ĺ� ��������ꡡ���� 2006ǯ��(PDF)
������ ��������ꡡ���� 06

2006ǯ�λ�����������ϡ����ܤ�����ѤޤǥХ�褯���ꤵ��Ƥ����Ȼפ��ޤ���
����Τۤ�������Ǥ⡢���Ū�䤵�������꤬����ޤ����顢
���ؤ����ʿͤǤ⤢����᤺�˺Ǹ�ޤ��ɤ������˥������Ƥߤ뤳�ȤǤ���
���������åפ���Ǥ��礦��
ʸ���μ��ư�̣��ͤ����ɤ�Ĥ֤���������Ȼפ��ޤ�����
���ΰ�̣��ͤ�����������Ȥ��ơ������Ǥ���
�����������λ��ͤˤ������Ǥ���
�����4�����ä��Ǥ���
�����������̤��������Ѥδ֤˴ط�������ȤϤͤ���
������ ��������ꡡ���� 2006ǯ��(PDF)
ʡ�温 ��������ꡡ���� 06

2006ǯ��ʡ�温������ϡ����ܤ�����ѤޤǥХ�褯���ꤵ��Ƥ����Ȼפ��ޤ���
4��5������Ͼ�������ǡ����⾯���ѻ��ˤʤäƤ��ޤ���
�����餺���ä�����ߤ����Ȼפ��ޤ���
�Ŀ�Ū�ˤ�5�����꤬�ڤ���ޤ�����
ʡ�温 ��������ꡡ���� 2006ǯ��(PDF)
��� ��������ꡡ���� 06

2006ǯ�����������ϡ���顢�������꤬������������٤������Ȼפ��ޤ�����
�����6��7������������Ȼפ��ޤ�����
����ο��ؤϡ�����η���ʤ��ƤϤ����ʤ����꤬����ޤ���
����Ǥ��ä����ʤ����֤������ꤽ���Ǥ���
����Ū�ʻͤ��ܤ����Ȥ�����̣�ǤϤ������Ȥ��Ȥ��⤤�ޤ�����
�����Ǥ������ΤϤ���äȤ��襤�������Ȼפ��ޤ���
�����⡢����η��Ϥɤ���������Ū�˽٤��ʤΤ������ޤ��Ǥ���
���ä��꺬���������η���Ȥʤ�ȡ����ʤ�λ��֤���䤹���Ȥˤʤ�ޤ�����������
��� ��������ꡡ���� 2006ǯ��(PDF)
�ٻ��� ��������ꡡ���� 06

2006ǯ���ٻ���������ϡ��������꤫��������ޤ����������ꤵ��Ƥ��ޤ�����
���̴֤Ǻ����Ĥ�������Ȼפ��ޤ���
�����4��5��6�κǸ�����꤬���餹������̤Ϥʤ��ʤ����ʤ��Ǥ��礦��
���줬����ʤ����٥�ˤʤ�ȡ����ؤǺ���Ĥ��뤳�Ȥ��Ǥ��ޤ���
���ʤߤˡ��錄����6��(3)�������20ʬ���餤Ǻ�ߤޤ�����
����֤ǤϤ���ʤ�Ǻ�ळ�ȤϤǤ��ʤ��Ǥ��礦���顢
¿�������̤ˤȤäƤϡ��֤Ǥ��ʤ��Ƥ����פȳ���ڤ�٤�������Ȼפ��ޤ���
������ּΤƤ�����פǤ���
�����ͤ��뤯�餤���ä��顢�ۤ���ʬ���ꤽ��������˻��֤�䤯�٤��Ǥ���
�ٻ��� ��������ꡡ���� 2006ǯ��(PDF)
���㸩 ��������ꡡ���� 06

2006ǯ�ο��㸩������ϡ����Ū�䤵����������ä��Ȼפ��ޤ���
����������Ͻ��ꤵ��Ƥ��ޤ���Ǥ�����
����夤�ơ��ߥ��ʤ����Ȥ�����ˤʤ�ƥ��ȤǤ���
���㸩 ��������ꡡ���� 2006ǯ��(PDF)
����� ��������ꡡ���� 06

2006ǯ�ο����������ϡ��ä����Ȥ��ä����꤬���ꤵ��Ƥ��ޤ���Ǥ�����
���ؤ����դʿͤ����Ǥ��ޤ꺹���Ĥ��ʤ��ƥ��Ȥ��ä��Ȼפ��ޤ���
ȿ�Фˡ�ɸ��Ū�����꤬¿���Τǡ�ʿ������٥�����̤����˺����Ĥ�������ä��ΤǤϤʤ��Ǥ��礦����
�ٶ�����С����������Ӥ䤹���ƥ��ȤǤ���
����� ��������ꡡ���� 2006ǯ��(PDF)
����� ��������ꡡ���� 06

2006ǯ������Ԥ�����ϡ����ɸ�ࡢ�������꤬���ܤǤ��礦����
���������ҤͤäƤ�������Ϥ���ޤ���Τǡ�
��ľ�˲������פǤ���
�Ŀ�Ū�����Ȼפä�����ϡ�4��(2)�����ꡣ
�Ѥ������ʤ��顢������ʬ���餺��15ʬ���餤�ͤ��Ƥ��ޤ��ޤ�����
ʬ���äƤ��ޤ��д�ñ�ʤΤǤ����ɤͤ���
����� ��������ꡡ���� 2006ǯ��(PDF)
������Ԥ���������������ʸ������Ƥ��ޤ���ʿ��18ǯ����Ω�����ع����ϸ�������ڤ������˷Ǻܤ���Ƥ��ޤ���
���ո� ��������ꡡ���� 06

2006ǯ�����ո�������ϡ���ľ�����꤬¿���Ȼפ��ޤ�����
���ؤδ���Ū���μ����ȤˤĤ��Ƥ���С������꤬�濴�Ǥ���
�Ҥͤ��줿����⤢��ޤ���Ǥ�����
���ʤȻפä��Τϡ�5��(2)������Ǥ����͡�
���������Τ϶��ʽ�˺ܤäƤʤ��Τǡ�
�ɤ���äƤ��������äѤ�ʬ����ʤ��Ȥ����ͤ����뤫�⤷��ޤ���
�ҥ�Ȥ��Ȥˡ�ʬ���뤳�Ȥ����Ĺ����Ƥ������Ф����ޤ�ޤ���
���ո� ��������ꡡ���� 2006ǯ��(PDF)
��̸� ��������ꡡ���� 06

2006ǯ�κ�̸�������ϡ��Ҥ꤬ͤ�����Ƥ��ޤ��͡�
�褯��������ǤϤʤ��Τǡ���֤��졩�Ȼפ�����ɡ�
�������ͤ��Ƥߤ�Ȳ�ˡ���פ��⤫��
�Ȥ����褦�����꤬��������ޤ�����
�Ŀ�Ū�ˤϲƤ����������ä��Ǥ���
�������ʤ��顢���ؤ��������̤ˤȤäƤϡ�����äȤ�ä����Ǥ��͡�
����Τ������ŵ����Ƥ��ޤ����Ȥ��ä�������Ǥ�û���֤Ǥ������Ǥ��Ǥ��ʤ��Ȼפ��ޤ���
���ʤ��ٶ��ǡ�
����η���ʤ������ʤ�Τ�����ͳ��ͤ��ʤ��顢
��ǫ�����Ƥ����Τ��褤�Ǥ��礦��
�������֤Ǥ�
�֤�������������⡢���������ʬ����ʤ����פȤʤäƤ��ޤ���ǽ���⤢��ޤ���
�ѥ˥å��ˤʤ�ʤ��褦�ˤ������Ǥ���
ʿ�����Ϥ���ۤɹ⤯�ʤ��Ϥ��Ǥ���
���ˤȤ��Ƥϡ��������ߥ��ʤ����ä����롣�������������ȥ饤��
���Ȥϡ����Ū�䤵�����Ȼפ�������伫ʬ�����դ�������İ�IJƤ�����
�Ȥ����Τ������Ȼפ��ޤ���
��̸� ��������ꡡ���� 2006ǯ��(PDF)
��̸�Ω���綵�饻������������ˡ������������������⤬����ޤ������������Τ�����ȡ����˻��ͤˤʤ�ޤ��͡��������ΤˤȤäƤ⤢�꤬�����Ǥ���
���ϸ� ��������ꡡ���� 06

2006ǯ�η��ϸ�������ϡ�����٤ΥХ���褤�ȴ����ޤ�����
2��(5)�έ�������Ϥ���äȼꤴ�襤���⡣
������μ���ȻȤ������ΤäƤ���Фʤ�Ƥ��ȤΤʤ�����ʤΤǤ�����
�Ƕ�ϻȤ����ˤ�����ä����꤬�ʤ����ᡢ�ΤǤ��Ƴ���Ƥ��ޤ���
�̤˶����Ƥ⤤���ΤǤ������ۤ��ˤ�ꤿ�����꤬��������ޤ����鎥������
Ʊ���褦��������¿���ΤǤϤʤ��Ǥ��礦����
���Ȥ�6(2)�������ä��Ǥ���
����Ϥʤ��ʤ��ʤ��������ʤ���
���ϸ� ��������ꡡ���� 2006ǯ��(PDF)
�����,����,���ϸ�,���,�����,����,�ؽ�
���ڸ� ��������ꡡ���� 06

2006ǯ�����ڸ�������ϡ�������̤�¿���ȴ����ޤ�����
���ؤ����դʿͤǤ⤳���50ʬ�Ǥ��Τ���ľ���äƤĤ餤�Ȼפ��ޤ���
100�����äƤ����ȡ����֤���ʤ��ƶ줷�ळ�Ȥˤʤ꤫�ͤޤ������դ�ɬ�פǤ���
���Ʋʤ�����������ϡ����������Ф���
�����äơ���ñ������ޤ���Ȥ��Ƥ��ޤ����ȤΤʤ��褦�ˡ�
���γ�꤭�꤬�ο����Ȼפ��ޤ���
���ؤ����ʿͤ�����ꡢ��������ä����뤳�Ȥǡ�����������褦�ˤʤäƤ��ޤ���
���ڸ� ��������ꡡ���� 2006ǯ��(PDF)
��븩 ��������ꡡ���� 06

2006ǯ�ΰ�븩������ϡ����ܤ����������ޤǥХ�褯���ꤵ��Ƥ���Ȼפ��ޤ�����
���ؤ����ʿͤϡ�������ä����롣
���ؤ����դʿͤϡ�100�������äƤ��äƤ⤤�����⤷��ޤ���
�äˡ֤���Ϥ���äȲʤ��������ʤ����������פȤ������꤬����ޤ���
���ʤȻפä�����ϡ�3��(1)��
10a��b��10b��a��1�����줾�첿���̣����Τ���ʬ����ʤ��ȡ�����äȲΤ��Ĥ餤�������Ȼפ��ޤ�����
8��(2)�����Ǥ����������Ȳ�������Ϥ��ä������ޤ����顢
���ؤ����դ����̤ˤϤ��ҤȤ⤽�Υ�٥�ޤǤ��ä��ߤ����Ȼפ��ޤ���
��븩 ��������ꡡ���� 2006ǯ��(PDF)
ʡ�縩 ��������ꡡ���� 06

2006ǯ��ʡ�縩������ϡ����ܤ����������ޤǥХ�褯���ꤵ��Ƥ���Ȼפ��ޤ�����
�����Ĥ������ޤޤ�Ƥ��ޤ�������˻��֤��������¾�δ�ñ���������֤��ʤ��ʤäƤ��ޤ��ޤ����顢���դ�ɬ�פǤ���
����Ȥ϶���Ū�ˤ�3��(3)��6��(2)�ʤɤǤ���
�錄���Τ�����ǤϷ���ͤ�����ʣ���ʤΤǡ�
�⤦������ñ�ʲ�ˡ�ʤ���Τ��ȹͤ���Ǥ���
ʡ�縩 ��������ꡡ���� 2006ǯ��(PDF)
������ ��������ꡡ���� 06

2006ǯ�λ�����������ϡ��ȤƤ�䤵�����ä��Ȼפ��ޤ���
�ܾ븩�����ĸ�������Τ褦�ʡ�Ķ����פȸ�����ΤϤ���ޤ���Ǥ�����
���������ƥ��ȤǤϡ������쥹�ߥ������ݤ�ʬ�����ꤷ�ޤ��Τǡ�
����Ū�ʷ���μ¤ˤ�뤳�Ȥ����פˤʤ�Ǥ��礦��
�Ŀ�Ū�ˤ�4��2��(2)�����꤬�ʤ�ۤɤȻפ��ޤ�����
4��1��ͶƳ����ˤʤäƤ���ΤǤ�����
�����Ǥʤ���С����ʤ�Ǻ��Ϥ��Ǥ���
������ ��������ꡡ���� 2006ǯ��(PDF)
���ĸ� ��������ꡡ���� 06

2006ǯ�ν��ĸ�������ϡ������̤��ȤƤ�¿���Ǥ���
�ǽ餫��硹�ˡ��Ȥ�äƤ���ȡ����֤��ʤ��ʤäƤ��ޤ���ǽ��������ޤ����顢
��������ˤ���ʤɤι��פ�ɬ�פǤ���
5��(3)���������ȴ����ޤ�����
���ĸ��β��ͤ������������Ǥ��礦����
���ĸ� ��������ꡡ���� 2006ǯ��(PDF)
�ܾ븩 ��������ꡡ���� 06

2006ǯ�٤εܾ븩�ο��ؤϺ�ǯ�˰���³�����������ʤäƤ��ޤ���
����Ū�ʻͤ�ɬ�פȤ����褦�˻פ��ޤ���
�ܾ븩�Τۤ��ζ��ʤ�����ϸ��Ƥ��ޤ���
���ؤ��礭�������Ĥ��Τϴְ㤤�ʤ������Ǥ���
�ܾ븩 ��������ꡡ���� 2006ǯ��(PDF)
��긩 ��������ꡡ���� 06

��긩��2006ǯ��������̤�¿���Ǥ��͡�
�����50ʬ�DzΤϤ��ä������ѤǤ��礦���ǽ餫����֤˲Ƥ���ȡ����֤��ʤ��ʤäƤ��ޤ����Ȥ⤢��Ȼפ��ޤ���ʬ���ꤽ�������꤫���˼��Ĥ��Ƥ����Τ������Ȼפ��ޤ���
����٤Ȥ��Ƥϡ��������꤫���������ޤǥХ�褯���ꤵ��Ƥ��ޤ���
��긩 ��������ꡡ���� 2006ǯ��(PDF)
�Ŀ��� ��������ꡡ���� 06

�Ŀ�����2006ǯ�٤�����ϡ��������꤬���ʤ����������꤬¿���ä��褦�Ǥ���
���������ƥ��Ȥϡ����ؤ��������̤ˤȤäƤϸ������Ǥ��͡�
��������Ǥ��ä���������Ȥꡢ���դ�ʬ��(������ؿ�(y=ax2)�ʤ�)�����䤷�Ƥ����Ȥ����Ȼפ��ޤ���
���ؤ����������Ǥ������̤����δ֤Ǻ����Ĥ��ޤ���
���ؤ����դ����ȸ����ͤ��������ܻؤ��ޤ��͡�(4��5�����餹��Ǥ����ʸ�礢��ޤ���͡�)
�Ŀ��� ��������ꡡ���� 2006ǯ��(PDF)
�̳�ƻ ��������ꡡ���� 06

�̳�ƻ����������ˤ䤵��������������꤬�Х�褯���ꤵ��Ƥޤ��͡�
���̤μ��Ϥ˹�碌�ơ������Ĥ��䤹���ΤǤϤʤ����Ȼפ��ޤ���
���̤ˤȤäƤ��ٶ�����С�����ʬ�������������Ӥ����ӤƤ����褦�ʡ�
����ʥƥ��Ȥ��Ȼפ��ޤ���
�Ŀ�Ū�ˤ�5����3�����꤬���ä��Ǥ���
���μ������Ϥ褯����ޤ������ʤ�ۤɤ�������Υҥ�Ȥ�������Ƴ����Τ��ȡ���������Ƥ��ޤ���
�̳�ƻ ��������ꡡ���� 2006ǯ��(PDF)
ư�������� 05���5
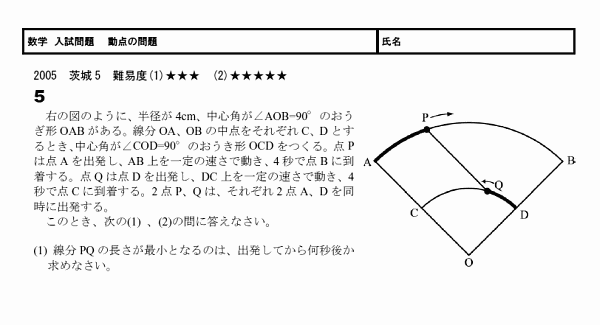
����ư������Ǥ���
���٤�ͤ���Ȥ���������Ū��ư��������Ȥ���äȰ㤦�Ȥ����Ǥ��礦����
�Ŀ�Ū�ˤ�(2)�����꤬�֤ʤ�ۤɡ�����������ʡפȻפ��ޤ�����
���ء���������� ư�������� 05���5������١���������(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
���������� ��ʿ�������� 05���7
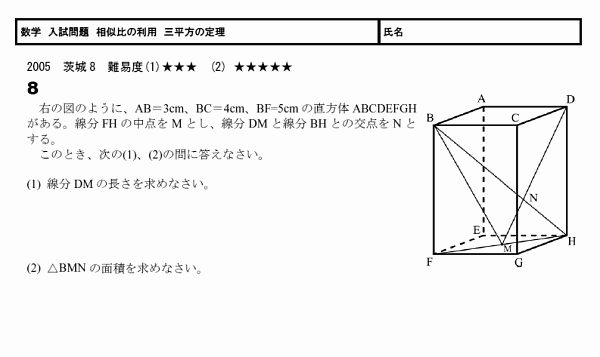
��������ˤ褯�Ф륿���פ�����Ǥ���
(2)�����Ѥ����Ȥ������������Ѥ��ޤ���
���ء���������� ���������� ��ʿ�������� 05���7������١�������(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
���Ⱦ��� ��� 05���7
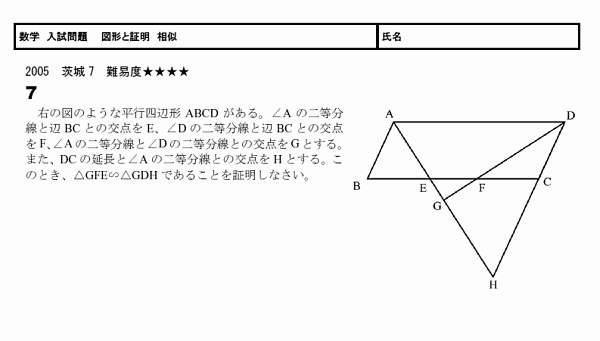
���ξ����Ͼ����λ��������̤꤫����ޤ���
���̤꤫�ξ����Τ��������ʷ�ʾ�����2�ĤǤ���
���ء���������� ���Ⱦ��� ��� 05���7������١�������(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
ʸ���μ� 05���6
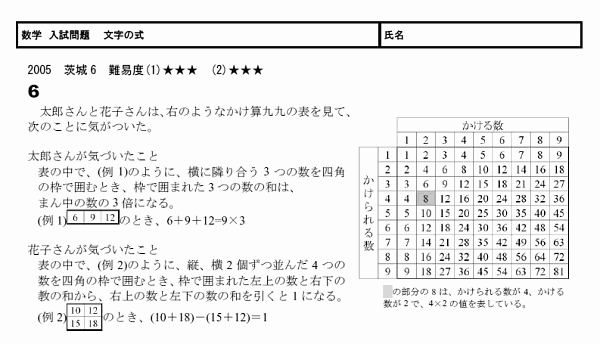
ʸ���μ�������Ǥ���
��������ǤϤ�������Ĺ��ʸ�Ϥ��ɤޤʤ���Фʤ�ʤ����Ȥ�¿���Τǡ�����Ƥ���ɬ�פ�����ޤ���
����夤���ɤ��ʬ����ޤ����顣
��������ϡ��츫�����Ǥ�������äƤߤ�Ф��ȳڤ˲ޤ��衣
(����Ǥ⡢ʸ���μ��ξ����ʤ���Фʤ�ʤ��Τǡ�
���������ʻҤˤȤäƤϤ��Ĥ�����Ǥ�����)
���ء���������� ʸ���μ� 05���6������١�����(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
2���ؿ� ���ѿ� 05���4
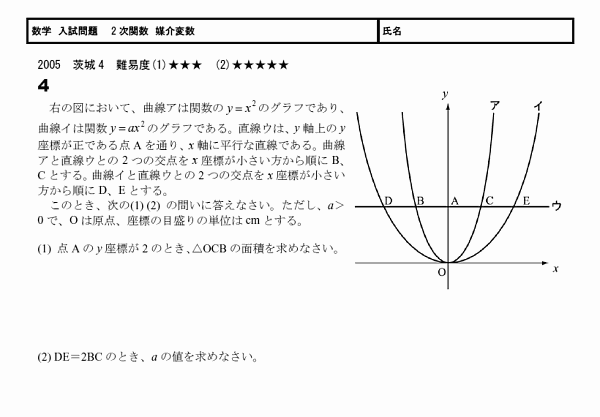
���ѿ����Ѥ��Ʋ�����Ǥ���
�����ޤ�������
�����κǸ�Τۤ����ޤ����äƤʤ��Ȥ������̤�¿���Ȼפ��ޤ���
����äȹ��פ���ȡ��ؽ��ϰ���Dz�ΤǤ����ͤ���
����Ȥ�ۤ��˴�ñ�ʲ��������뤫�⤷��ޤ���
���Ĥ����Ȥ��Ϥ��Τ餻����������
��09.01.29�ɵ�
����ꥫ�߽����а��ͤ�ꡢ��ñ�ʲ����Ҳ𤤤������ޤ�����
���꤬�Ȥ��������ޤ���
�ʲ��˰��Ѥ������ޤ���
�����ѳ��ϡ��������
��������ǯ�ΰ�븩�Σ��Ρʣ��ˤ�
�ش�ñ�ʲ����Ĥ������Ϥ��Τ餻���������٤Ȥ���ޤ����Τǥ����Ȥ����Ƥ���������
����ʸ���ɤ�¤�A�Σ���ɸ�ϻ��꤬�ʤ�����������ʸ�Ǥϡ�a���ͤ���ޤ�С�DE��BC�����A�Σ���ɸ�˴ؤ�餺����Ǥ���٤Ȥ����Τϴ��ΤȤ��Ƥ��ɤ��褦�˴������ޤ�����
�⤷�����ͤ����ñ�ˡ���������ļ������Ǥ褤�褦�˻פ��ޤ�����
�Ĥޤꡢ
C�ʣ������ˤλ���ͤ���ȡ���E�ϡʣ������ˤˤʤ�Ϥ��ʤΤǡ�
a=1/4
�Ȥ����˽Ф��Ƥ��ޤäƹ���ʤ��褦�˴����ޤ�����
C���ʣ������ˤǤ�ʣ������ˤǤ�Ʊ�ͤˤʤ뤳�Ȥ��ǧ����С�������Ǥ�ξڤ�������Τ��ʤȡ�
���ʤ��Ȥ��a���ͤ���ޤ�С�DE��BC�����A�Σ���ɸ�˴ؤ�餺����Ǥ���٤��Ȥξ���������Ƥ���櫓�Ǥ�ʤ��ΤǤ���������μ����ᤵ���櫓�Ǥ�ʤ��Τǡ�����Ū�ˤϤ���ǹ���ʤ��褦�˴����ޤ�����
���뤤���ѿ������ɸ�ˤ�����ǡ�C�Σ���ɸ���Ȥ��ơ�
S��2���a�ߡС�2S�ˤ�2���
��S�ϣ��Ǥʤ��Τ�a=1/4�ȸ�����������ȳؽ��ϰ���ˤʤ�ޤ����Ǥ��礦����
�ʤ���äȹ��פ���ȡ��Ȥ����ΤϤ��Τ�����Ǥ��礦������
���������Ѥ����ޤ�
�ޤä������ä�����̤�Ǥ���
���ѿ���x��ɸ���Ѥ��뤳�Ȥǡ�����ʣ���ˤ����ˤ��ߤޤ���
���Ѥ������ʤ��顢�����ϵ����Ĥ��ޤ���Ǥ�����
HP�˷Ǻܤε��Ĥꤤ���ޤ����顢
�ʲ��Τ��ֻ��������ޤ�����
�����ѳ��ϡ��������
����®�Τ��ֻ�ͭ�������ޤ�����
����β��������ͤˤʤ�ޤ����顢���줷���פ��ޤ���
�����Ĥ����̤�
���ؤ褯ʬ����ʤ����ϴ�ñ�ˤ��ơ�����Ū������ñ����Ǥɤ��ʤ뤫��ͤ��褦����
���ȸ��äƤ��ޤ���
���äˡ�����������٤�ص�§��������٤λ������Ω�Ĺͤ����Ȼפ��ޤ�����
����������ˤĤ��Ƥ⡢�������٤��ƤϤޤ���ʬ�����뤫�ȴ���������Ǥ���
������Ū���ͤǹͤ��ơ���§�������뤳�Ȥ��ߤ���С��ѿ��ƤƤߤ�ͤ��ˤĤʤ���褦�ˤ��Ĥⴶ���Ƥ��ޡ���������Ū��ǹͤ����������Τޤޡ��ѿ���Ȥä�����Ĥ���ҥ�Ȥˤ�ʤ뤫�Ȼפ��ޤ���
��ʸ�Ϥ��ۤ��Ƥ��Ѥ��������¤�Ǥ��������ͤΤ���ˤ��Ƥ�ΤǤ��������HP�˺ܤ��Ƥ��������Τϰ���˹����ޤ���
���������Ѥ����ޤ�
��⡢�ֶ���Ū�ʿ���������ƹͤ��Ƥߤ褦�פȻ�Ƴ���Ƥ��ޤ���
����ʤΤˡ������Ĥ����Ȥ�����ޤ���Ǥ�������������
�ؿ��ΤȤ��ˤ⤹�������ѿ�����餺�ˡ�����Ū�ʿ����ǹͤ��Ƥߤ�٤��Ǥ��͡�
�����ٶ��ˤʤ�ޤ�����
�а��ͤ��꤬�Ȥ��������ޤ�����
���ء���������� 2���ؿ� ���ѿ� 05���4������١���������(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
����05���3(3)

��Ψ�����ꡣ
���ʤ��ߡ������������Ĥ��ꤲ������Ǥ���������Ȥ����Ȥ���������äȤ���ʣ���Ǥ���
���ݤ������餺�˳μ¤˿����ޤ��礦��
���ء���������� ��Ψ��05���3(3)������١�����(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
���ѡ�05���3(2)
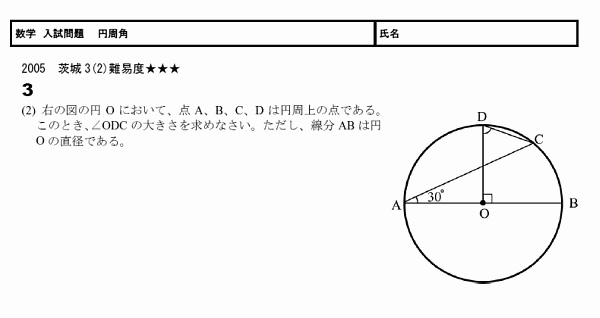
���٤��������Ǥ���
�����������̤�����Ǥ������Ϥޤ�ͤϤϤޤ�ޤ���
�֤�����60�뤸��ʤ��Ρ��פȤ����ͤϡ����Ѥ��濴�Ѥδط���Ĥ���Ƥ��ޤ���衣
��ˡ֤ɤθ̡��פȹͤ���Ȱ��ä����餺�ˤ��ߤޤ���
�Ĥޤ�֤ɤθ̤��б����Ƥ�����Ѥ��ס��֤ɤθ̤��б����Ƥ����濴�Ѥ��פ�ͤ��뤳�ȤǤ���
���ء���������� ���ѡ���롡05������١�����(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
�������������ѡ���롡05

�褯��������Ǥ���
���������Ϸ����Ǥ��Ƥ�ʸ����(��������������)�ˤʤ�Ȥޤä����꤬�Фʤ��Ȥ������̤������ΤǤ���
��������̤ϡ��ޤ��϶��ʽ�������Ф���Τ�����Ǥ���
��븩�Τ�������϶��ʽ��٥�Ǥ��Τǡ����ä���ޥ��������Ƥ��������Ǥ���
���ء���������� �������������ѡ���롡05������١�����(PDF)
�������2005ǯ�� ��븩 ��������ꡡ�����ء�
����� ���� �������ꡡ��롡05

��븩�ι��������δ��������ޤ�����
��븩�϶��ʽ��٥�δ������꤬����������ꤵ��Ƥ���褦�Ǥ���
���ؤ��������̤ˤȤäƤϽ��������䤹���ΤǤϤʤ��Ǥ��礦����
���ʽ�������ޤ����ä���Ǥ���褦�ˤ��롢�Ȥ�����ɸ��Ω�Ƥ䤹���Ǥ����顣
���ء������������ش������ꡡ��롡05(PDF)
�������2005ǯ�� ��븩 ��������ꡡ������
��븩 ��������ꡡ���� 05

2005ǯ�ΰ�븩������ϡ�������̤�¿���Ǥ��͡������50ʬ�DzȤʤ�ȡ�����äȤ��Ĥ����⤷��ޤ����������ɤ������ơ���������˻��֤��뤫���ݥ���ȤǤ��礦����
��������Ȥ��äƤ⡢����Τ褯�Ф륿���פ����꤬�濴�Ǥ���
������к��Ȥ��Ƥϡ����μ������ˤ褯�Ф������¿�������äơ��ѥ������Ĥ���Ǥ����Ȥ����Ȼפ��ޤ���
��븩 ��������ꡡ���� 2005ǯ��(PDF)
��ʿ�������� ��äȤ�û���ʤ�Ȥ� 05 ʡ��
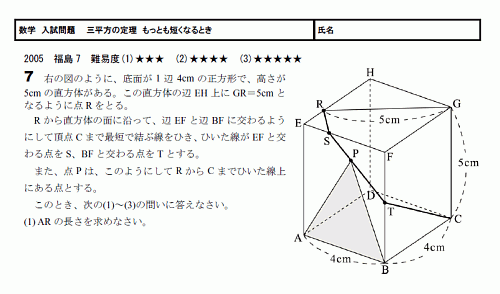
���ء���������ꡡ��ʿ�������� ��äȤ�û���ʤ�Ȥ���05ʡ�縩7 ����١���������(PDF)
��������Ϥʤ��ʤ����Τ�������Ǥ���
���Ȥ��äơ�����ʣ���ˤʤ��ʤ������Ѥ���������Ȼפ��ޤ���
���ؤǺ���Ĥ��������̤ˤϤ��Ҳ��ߤ������ꡣ
���ء���������ꡡ��ʿ�������� ��äȤ�û���ʤ�Ȥ���05ʡ�縩7 ����١���������(PDF)
�������05ʡ�縩�����ء������������
���������� 05 ʡ��
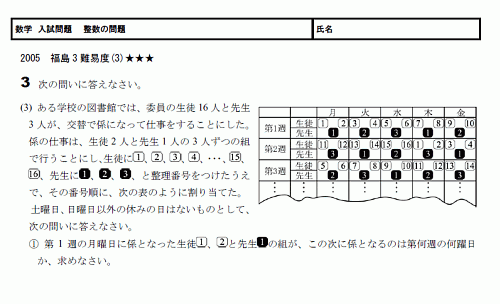
���ء���������ꡡ���������ꡡ05ʡ�縩3(3) ����١�����(PDF)
�������ˤ���ꤵ�줽��������Ǥ�
�Ǿ����ܿ��ʤɤιͤ������Ȥ��ޤ�����
��ʬ�ǰ���ʬ����䤹����ˡ��õ���Τ������⡣
���ء���������ꡡ���������ꡡ05ʡ�縩3(3) ����١�����(PDF)
�������05ʡ�縩�����ء������������
��Ψ 05 ʡ��

���ء���������ꡡ��Ψ��05ʡ�縩3(2) ����١�����(PDF)
ɽ���ʬ����䤹���Ǥ���
?��������������Ƥ������ԻĤʴ��������ޤ���
���ء���������ꡡ��Ψ��05ʡ�縩3(2) ����١�����(PDF)
�������05ʡ�縩�����ء������������
ʸ���μ� 05 ʡ��
���� 05 ʡ��

���ء���������ꡡʸ���μ���05ʡ�縩2(4) ����١���(PDF)
ʸ���μ�������Ǥ���
�ޤ������ꡢ���ˤ���ʸ���ˤĤ��Ʋޤ���
���ء���������ꡡʸ���μ���05ʡ�縩2(4) ����١���(PDF)
�������05ʡ�縩�����ء������������
���� 05 ʡ��
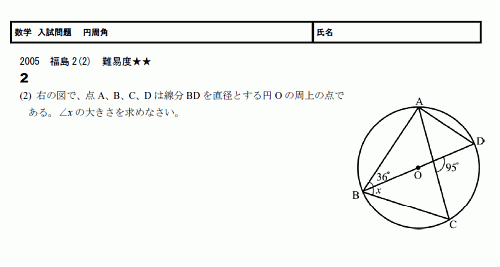
���ء���������ꡡ���� 05ʡ�縩2(2) ����١���(PDF)
���Ѥ�����Ǥ���
ľ�¤α��Ѥ�Ȥä���������Ǥ���
���ء���������ꡡ���� 05ʡ�縩2(2) ����١���(PDF)
�������05ʡ�縩�����ء������������
05ʡ�縩�����ء����������
ʡ�縩������ϡ��������꤫���������ޤǥХ�褯���ꤵ��Ƥ���ȴ����ޤ�����
��������Ǥ�����
����� ���������ѡ���ʿ��������(05����)
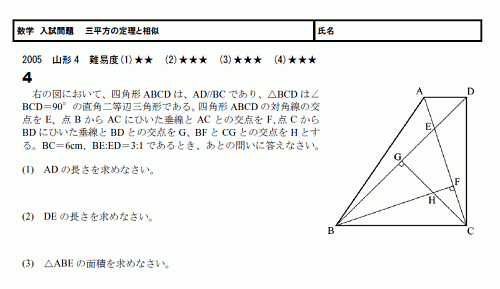
���ء���������ꡡ���������ѡ���ʿ�������� 05������4 ����١�����(PDF)
���ˤ褯���ꤵ��륿���פ�����Ǥ���
���⤽��ۤ�ʣ���ǤϤ���ޤ���Τǡ����٤�����Ǥ���褦�ˤ��Ƥ��������Ǥ���
�����������϶��ʻҤ�¿���Ǥ���
�����졢���ֵ̹��Ȥ��ơ��ץ��Ȥ�����������Ǥ���
���ء���������ꡡ���������ѡ���ʿ�������� 05������4 ����١�����(PDF)
�������05�����������ء������������
����� ����դ�����(05����)
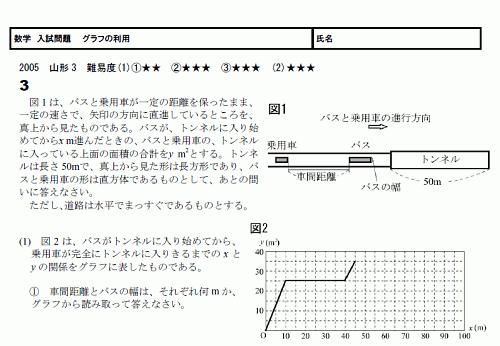
���ء���������ꡡ����դ����� 05������3 ����١�����(PDF)
��������ˤ褯�Ф륰��դ����Ѥ����ꡣ
��������⡢�ޤ����ܤǤ���
�Ǹ������Ǥ���(2)�����ͤ������ʤ��褦�ˎ�������
��������Ƥ���ͤ���ȴ�ñ�Ǥ����顣
���ء���������ꡡ����դ����� 05������3 ����١�����(PDF)
�������05�����������ء������������
����� ����դ�����(05����)

���ء���������ꡡ����դ����� 05������3 ����١�����(PDF)
��������ˤ褯�Ф륰��դ����Ѥ����ꡣ
��������⡢�ޤ����ܤǤ���
�Ǹ������Ǥ���(2)�����ͤ������ʤ��褦�ˎ�������
��������Ƥ���ͤ���ȴ�ñ�Ǥ����顣
���ء���������ꡡ����դ����� 05������3 ����١�����(PDF)
�������05�����������ء������������
����� ����������(05����)

���ء���������ꡡ���������� 05������2(4)A ����١�����(PDF)
�ԳФˤ�ɤ���ä��餤���Τ������ˤ�ʬ����ޤ���Ǥ�����
15�ä��餤Ǻ�����������
������ʬ����Ф��äȤ����֤ˤǤ���ΤǤ����͡�
(���ƥ��꤬�⤦�ҥ�ȤˤʤäƤ롦����)
���ء���������ꡡ���������� 05������2(4)A ����١�����(PDF)
�������05�����������ء������������
����� ���� �����ջ��ѷ�(05����)
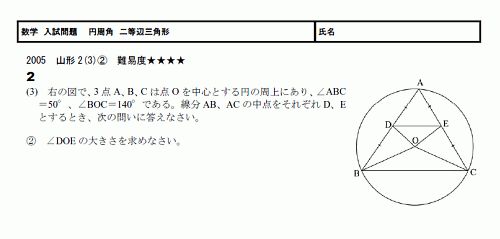
���ء���������ꡡ���� �����ջ��ѷ� 05������2(3) ����١�������(PDF)
���� �����ջ��ѷ������Ѥ��Ʋޤ���
����ä������⤷��ޤ���
���ء���������ꡡ���� �����ջ��ѷ� 05������2(3) ����١�������(PDF)
�������05�����������ء������������
����� ���� ����Ϣ������(05����)
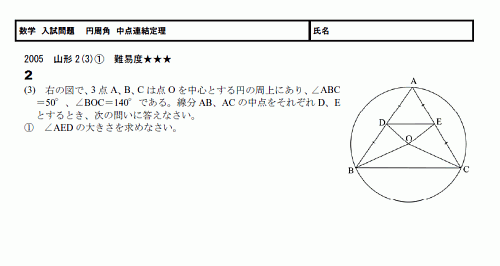
���ء���������ꡡ���� ����Ϣ������ 05������2(3) ����١�����(PDF)
���� ����Ϣ������������Ǥ���
�Ѥ��礭����������ꡣ
���ء���������ꡡ���� ����Ϣ������ 05������2(3) ����١�����(PDF)
�������05�����������ء������������
����� ϢΩ������������(05����)

���ء���������ꡡϢΩ������������ 05������2(2) ����١�����(PDF)
ϢΩ�����������Ѥ�����Ǥ���
�������ľ�����ꡣ
?��?������äȹ��פ���Ƥ������Ǥ���
?�ʤϤ�������Ƥ��äƤ���ͤ��륿���פοͤˤ�����ʤ������顣
���ء���������ꡡϢΩ������������ 05������2(2) ����١�����(PDF)
�������05�����������ء������������
��ʿ�������������ѡ�05����

���ء���������ꡡ��ʿ�������������� 05������2(1) ����١�����(PDF)
��������⤤��������Ȼפ��ޤ�����
������������ϤҤ꤬ͤ��ľ�Ǥ���
���ؤ��������̤ˤ�餻�����Ǥ��͡�
���ؤ��������̤������Ǥ��������꤬��ڤ�����̣�廊��������Ȼפ��ޤ���
���ء���������ꡡ��ʿ�������������� 05������2(1) ����١�����(PDF)
�������05�����������ء������������
����� ��ʪ���ȿ�(05����)

���ء���������ꡡ��ʪ���ȿ� 05������1(5) ����١�����(PDF)
����ʸ�ˤ��뤤����ʥҥ�Ȥ��Ȥ߹�碌�ơ�
����ˤ��ɤ�Ĥ��Ȥ����Τ����ؤ������������Ȼפ��ޤ���
��������Ϸ���ʣ���ˤʤ餺��������������������褤������Ȼפ��ޤ���
���ء���������ꡡ��ʪ���ȿ� 05������1(5) ����١�����(PDF)
�������05�����������ء������������
����� ��Ψ(05����)
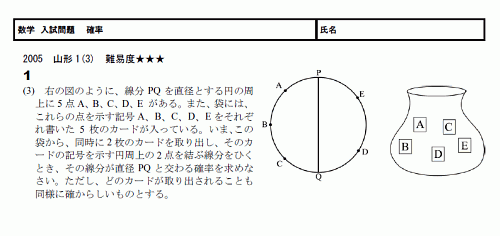
���ء���������ꡡ��Ψ 05������1(3) ����١�����(PDF)
��Ψ������Ǥ���
��İ�Ĥξ���ͤ��Ƥ����С�����ۤ����Ϥ���ޤ���
���ء���������ꡡ��Ψ 05������1(3) ����١�����(PDF)
�������05�����������ء������������
����� 05����������������

���ء���������ꡡ05���������������ꡡ����١����ʲ�(PDF)
����������δ�������Τߤ�ޤ�����
���ء���������ꡡ05���������������ꡡ����١����ʲ�(PDF)
�������05�����������ء������������
05�����������ء����������
2005ǯ�λ�������������ä��������ʤ�����ľ�������濴�ν���Ǥ�����
���ʽ���濴�ˤ��ä����ٶ���ʤ�Ƥ������Ȥǽ�ʬ���б��Ǥ�������Ǥ��͡�
ȿ�̡����ؤ����դ����̤ˤ�ʪ��ʤ����⤷��ޤ���
����� ��§�������� (05����6��?)
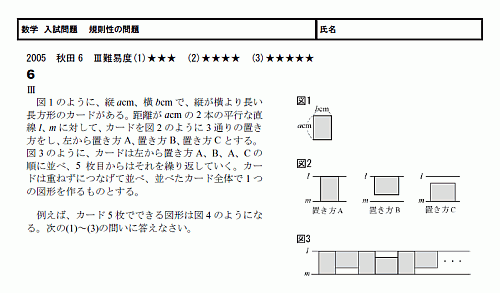
���ء���������ꡡ��§�������� 05���ĸ�6��? ����١���������(PDF)
����ϡ��Ŀ�Ū�ˤϤȤƤ���������Ǥ�����
�����˸����ơ����Ĥ�ñ��ʵ�§��������Ȥ��������ä��Ǥ���
(3)�Ϥ��ä������ݤ������Τdzи礬ɬ�פǤ���
���ء���������ꡡ��§�������� 05���ĸ�6��? ����١���������(PDF)
�������05���ĸ������ء������������
����� ��§�������� (05����6��?)

���ء���������ꡡ��§�������� 05���ĸ�6��? ����١�������(PDF)
���ꤽ�Τ�ΤϤ����Ȥ������⡢
����ʸ������Τ����Ȼפ��ޤ���
��İ����ǫ���ɤ߿ʤ�ƹԤäƤ���������
���ء���������ꡡ��§�������� 05���ĸ�6��? ����١�������(PDF)
�������05���ĸ������ء������������
����� ��§�������� (05����6��?)

���ء���������ꡡ��§�������� 05���ĸ�6��? ����١�����(PDF)
��§�������ꡣ
��������ϡ����Ū�פ������褤������Ȼפ��ޤ���
�������Ǥ⡢��ĥ��ФǤ���Ȥ���������§��������Τ����Ȥ����Ǥ���͡�
���ء���������ꡡ��§�������� 05���ĸ�6��? ����١�����(PDF)
�������05���ĸ������ء������������
����� ���������ѡ��� (05����)

���ء���������ꡡ���������ѡ��� 05���ĸ�5 ����١���������(PDF)
��Ʊ�ʻ��ѷ���ߤĤ�������ʻ��ѷ��Ĥ��������ջ��ѷ��Ǥ��뤳�Ȥ˵����Ĥ���
�ȡ������ˤ�����ޤǤˤ�����ʤ��Ȥ�ȯ�����ʤ��ƤϤʤ�ޤ���
���ΤĤɡ�������ʬ����䤹�����ˤ��Ƥ����Ϥ�ɬ�פǤ���
�������꤬�Ǥ����顢�����Ϥ�����ȸ��äƤ����Ȼפ��ޤ���
���ء���������ꡡ���������ѡ��� 05���ĸ�5 ����١���������(PDF)
�������05���ĸ������ء������������
����� ����դ����� (05����)
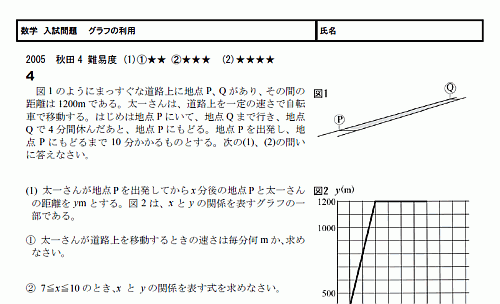
���ء���������ꡡ����դ����� 05���ĸ�4 ����١�������(PDF)
���μ�λ��֡���Υ��®���δط���դ�Ȥä�ɽ�������
�����ˤ褯���ꤵ��Ƥ��ޤ��͡�
���줫��⤳�η�����³���Ǥ��礦��
���ء���������ꡡ����դ����� 05���ĸ�4 ����١�������(PDF)
�������05���ĸ������ء������������
����� ��Ψ(05����)

���ء���������ꡡ��Ψ 05���ĸ�2(2) ����١�����(PDF)
��Ψ������Ǥ���
����äȤҤͤäƤ���ޤ��������Τ��餤�ΤҤͤ�ˤ��б������ߤ����Ǥ���
���ء���������ꡡ��Ψ 05���ĸ�2(2) ����١�����(PDF)
�������05���ĸ������ء������������
����� ��ʪ����ľ������ʬ����(05����)

���ء���������ꡡ��ʪ����ľ������ʬ���� 05���ĸ�1(13) ����١�����(PDF)
�����κ�ɸ�����Τ����ƤοͤˤϤ���äȤ�ä����Ǥ���
�����κ�ɸ���������⤢��ޤ�����
���ƤϤ�ƲƤ⤢�ޤ괶ư������ޤ���
ľ�ѻ��ѷ���Ƥߤơ����ȤäƵ���Τ���
����ʣ���ˤʤ�ޤ��������Ϥ��ä���Ȼפ��ޤ���
���ء���������ꡡ��ʪ����ľ������ʬ���� 05���ĸ�1(13) ����١�����(PDF)
�������05���ĸ������ء������������
����� ���������ѡ���ʿ��������(05����)
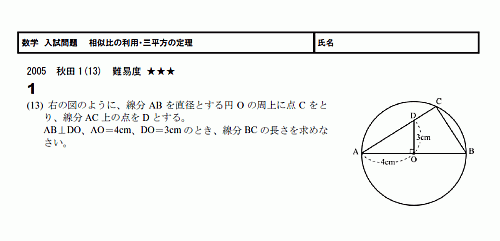
���ء���������ꡡ���������ѡ���ʿ�������� 05���ĸ�1(13) ����١�����(PDF)
���ۤ�������ޤ���ʣ��Ū���μ���ɬ�פȤ���Τǡ�
���Ȥ��ˤϤ��ä������줷�����⤷��ޤ���
�ֱ������꤬����äȶ��ǡ��������פȤ����ͤ����Υ����פ�������ϤDz�������ȡ������Ϥ��Ĥ��Ƥ��ޤ���
�����ϤȤϡ�ʬ���äƤ��뤳�Ȥ����������Ȥ�Ω�ƤƤ����Ϥȸ��äƤ⤤�����⤷��ޤ���
���ء���������ꡡ���������ѡ���ʿ�������� 05���ĸ�1(13) ����١�����(PDF)
�������05���ĸ������ء������������
����� ʸ���μ�(05����)

���ء���������ꡡʸ���μ� 05���ĸ�1(9) ����١�����(PDF)
����ʸ���鼰��Ĥ��äơ����μ���x�ˤĤ��Ʋޤ���
�ɤ�������äȤ���ʣ���ˤʤäƤ��ޤ���
�ܼ�Ū�ˤϤ���ۤ����ʤ��ΤǤ�����
�����ѻ��ʤΤǡ�����Ψ���㤤�Ǥ��礦��
���ء���������ꡡʸ���μ� 05���ĸ�1(9) ����١�����(PDF)
�������05���ĸ������ء������������
����� ��ž�Τ�ɽ����(05����)

���ء���������ꡡ��ž�Τ�ɽ���� 05���ĸ�1(10) ����١�����(PDF)
��ž�Τ�ɽ���Ѥ��������Ǥ���
05ǯ������Ǥϴ�긩�Ǥ�ۤ�Ʊ�����꤬���ꤵ��Ƥ��ޤ��͡�
���ء���������ꡡ��ž�Τ�ɽ���� 05���ĸ�1(10) ����١�����(PDF)
�������05���ĸ������ء������������
����� ����ʬ��(05����)

���ء���������ꡡ����ʬ�� 05���ĸ�1(10) ����١�������(PDF)
����������ʬ�ह��٤���������ʬ���ʬ�ह��٤�����Ǻ�ߤޤ���
��
��������������Ȥ����ϡ�a, b, c ���줾����ͤ�ʬ����ʤ��Ƥ⡢a��b��c ���ͤʤ���뤳�Ȥ��Ǥ���Ȥ����Ǥ����Ȥꤢ���������꤫�鼰��Ĥ��äƤߤơ�į��Ƥߤ�Ȥ��졩�ȵ����Ĥ����Ȥ�����ޤ���(�Ȥޤ������ۤ�����ФǤ�����)
����������狼��ʤ��ȸ��ä�����Ĥ�Ƥ�������Ǥϲ���ʬ����ޤ��Ȥꤢ������������ʬ��ʬ���뤳�Ȥ��ɮ�ǽФ��Ƥߤ뤳�ȡ����줬��ʬ�ؤΥҥ�Ȥˤʤ�ޤ���
���ء���������ꡡ����ʬ�� 05���ĸ�1(10) ����١�������(PDF)
�������05���ĸ������ء������������
����� �����������(05����)
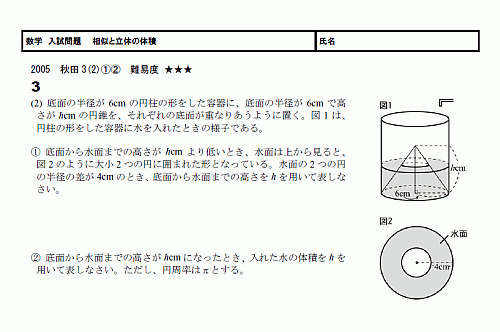
���ء���������ꡡ�����Ω�Τ����� 05���ĸ�3(2)?? ����١�����(PDF)
�ƴ����ο�����Ѥ�����Ǥ���
����ǤϤ��μ�������꤬�褯���ꤵ��ޤ�������������Ϥ��ۤ�������ޤ���
���ء���������ꡡ�����Ω�Τ����� 05���ĸ�3(2)?? ����١�����(PDF)
�������05���ĸ������ء������������
05���ĸ������ء����������
05���ĸ������ء����������
���ĸ�������Ϥʤ�������ޤ��͡�
���꼫�ΤϤ���ۤ����ʤ��ΤǤ���������ʸ������Τ˹����ޤ�ޤ���
�Ŀ�Ū�����ʤ��Ȼפä�����ϡ�6��?������Ǥ���
�츫ʣ�������˸����ơ��¤Ϥ����ȵ�§��¸�ߤ��Ƥ���Ȥ������������Ȼפ��ޤ���
����� ��ʿ���������ȱ� (05�ܾ�B)

���ء���������ꡡ��ʿ���������ȱ� 05�ܾ븩B5(3)? ����١�����������(PDF)
����������Ǥ�����
���Ѥ������ʤ��顢1���ְʾ�Ǻ�ߤޤ�����
�ޤ��ޤ�Ƭ���Ǥ��Ǥ���
������Ǥ����������꤬��ͤ�º�ɤ��Ƥ��ޤ��ޤ���
�̤˾��衢���餯�ʤ�ʤ��Ƥ⡢�������ʤ��Ƥ⡢
ñ��ˤ������Ȼפ���
��������������Ϥ���ˤ����Ǥ��礦�ͤ���
�����ⶵ�����ΤȤ��ơ���������������������Ƥ����Ǥ��ͤ���
(2008.3.19�ɵ�)
������ˡ��濴�Ѥ���뤳�Ȥ��Ǥ��ޤ��פȤ���ޤ��������ºݤˤϵ��뤳�Ȥ��Ǥ��ޤ���
�������Ƥ����ޤ�����
ü�����ޡ�����Ŧ���꤬�Ȥ��������ޤ�����
(2008.6.2�ɵ�)
����ü���ͤ�ꤴ��Ŧ���������ޤ�����
��Ϥ��濴�Ѥ���뤳�ȤϤǤ��ޤ���
�������Ƥ����ޤ�����
�ޤ�������˻�Ŧ���Ƥ��������Ƥ���ޤ�������
�������٤��ʤäƤ��ޤ��ޤ�����
����������ޤ���
�ʹ��������Ĥ��ˤʤäƤ��ޤ�������
���ء���������ꡡ��ʿ���������ȱ� 05�ܾ븩B5(3)? ����١�����������(PDF)
�������05�ܾ븩�����ء������������
����� ���������� (05�ܾ�B)
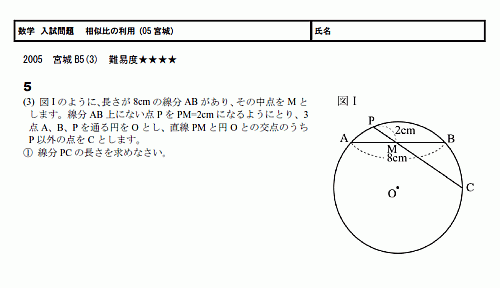
���ء���������ꡡ���������� 05�ܾ븩B5(3)? ����١�������(PDF)
ʬ���äƤ��ޤ��д�ñ�Ǥ�����ʬ����ޤǤ�������Ǥ���
�֤�����ľ�ѻ��ѷ��ǡ������פޤǹԤä���ͤ���Ǥ���
��äȥ���ץ�˲ޤ��衣
���ء���������ꡡ���������� 05�ܾ븩B5(3)? ����١�������(PDF)
�������05�ܾ븩�����ء������������
����� 2���ؿ� ���ѿ� (05�ܾ�B)
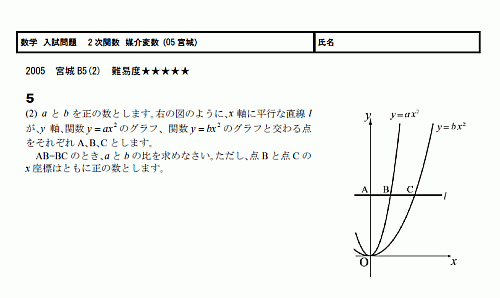
���ء���������ꡡ2���ؿ� ���ѿ� 05�ܾ븩B5(2) ����١���������(PDF)
���ѿ������ꡣ
�ɤ�����ѿ��ˤ�������֤褤�Τ�������ä�Ǻ�ߤޤ���
���⾯���ѻ��Ǥ��͡�
���ء���������ꡡ2���ؿ� ���ѿ� 05�ܾ븩B5(2) ����١���������(PDF)
�������05�ܾ븩�����ء������������
����� ��ʿ���������ȱ�(05�ܾ�)
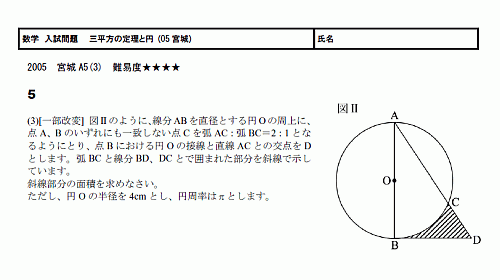
���ء���������ꡡ��ʿ���������ȱ� 05�ܾ븩A5(3) ����١�������(PDF)
���̤�ľ�ѻ��ѷ��Ĥ��뤳�Ȥ��Ǥ����Ⱦʬ�Ǥ����Ȥ������Ȥˤʤ�Ǥ��礦��
�̤�Ĺ�����椫�顢�Ѥ��礭����ʬ����ޤ���
����¿��Ĺ���ʤäƤ��ޤ��Τǡ����ߥ��ʤ��褦�ˡ�
������ʬ���äƤ���Τˤ⤫����餺���ߥ���������ȤʤäƤ��ޤ��Τϡ�
��������ä����ʤ��Ǥ���͡�
���ء���������ꡡ��ʿ���������ȱ� 05�ܾ븩A5(3) ����١�������(PDF)
�������05�ܾ븩�����ء������������
����� 2���ؿ������ѿ�(05�ܾ�)

���ء���������ꡡ2���ؿ������ѿ� 05�ܾ븩A5(2) ����١�������(PDF)
���ѿ���ȤäƲ�����Ǥ���
���ѿ������⤽��ऺ�����������ȤʤäƤ��ޤ�����
���ѿ���ɤ���äƻȤ�����ʬ���äƤ���Ф��Ȱפ�������ȸ����ޤ���
���ء���������ꡡ2���ؿ������ѿ� 05�ܾ븩A5(2) ����١�������(PDF)
�������05�ܾ븩�����ء������������
����� ���������ѡ���ʿ����������������(05�ܾ�)
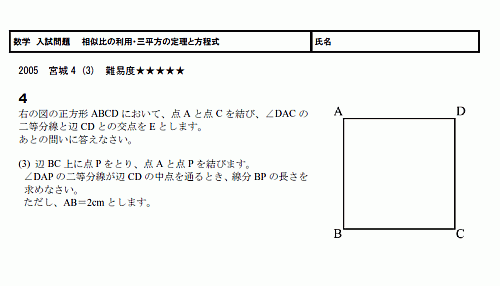
���ء���������ꡡ���������ѡ���ʿ���������������� 05�ܾ븩4(3) ����١���������(PDF)
������������Ǥ���
������ʲ��������ꤽ���Ǥ����顢
���椷�Ƥߤ�ȡ������Ȥ�ȯ���Ǥ������Ǥ���
���ؤ��Ϥ�Ĥ��Ǥ��礦�ͤ���
���ء���������ꡡ���������ѡ���ʿ���������������� 05�ܾ븩4(3) ����١���������(PDF)
�������05�ܾ븩�����ء������������
����� 05�ܾ븩����������

���ء���������ꡡ05�ܾ븩���������ꡡ����١������ʲ�(PDF)
�ܾ븩����δ�������Τߤ�ޤ�����
���ء���������ꡡ05�ܾ븩���������ꡡ����١������ʲ�(PDF)
�������05�ܾ븩�����ء������������
����� ʿ����(05�ܾ�)

���ء���������ꡡʿ���� 05�ܾ븩B5(1) ����١�������(PDF)
ʿ���������ꡣ
�褯�Ф�����ǡ��褯���䤵���ΤǤ���
�����������⤷�Ƥ�
���̤����������Ƥ���Τ���
���ޤ����褯ʬ����ʤ�����Ǥ���
���ޤ������Τ������Ϥʤ����ʤ���
���ؤΤ����������Ȥߤ����Ѥ���������Ȼפ�������ɤʤ���
���ء���������ꡡʿ���� 05�ܾ븩B5(1) ����١�������(PDF)
�������05�ܾ븩�����ء������������
����� ����դ�����(05�ܾ�)

���ء���������ꡡ����դ����� 05�ܾ븩3��(2)(3) ����١�������(PDF)
�ܾ븩�����ꡣ
�����ǤϤ����ޤ���͡�
���ء���������ꡡ����դ����� 05�ܾ븩3��(2)(3) ����١�������(PDF)
�������05�ܾ븩�����ء������������
����� ������������(���)

���ء���������ꡡ������������ 05�ܾ븩2��(1) ����١�����(PDF)
�����������Ѥ�����Ǥ���
ʸ���꤬���ʿͤ�¿���Ǥ��͡�
�Ƕ�ϡ��Ȥä����꤬���ʽ�ʤ��ʤ�ĤĤ���Τǡ�
����Ψ���Τ���٤Ʋ����äƤ���Τ��⤷��ޤ���
���ء���������ꡡ������������ 05�ܾ븩2��(1) ����١�����(PDF)
�������05�ܾ븩�����ء������������
����� 1���ؿ��δ��ä�����

���ء���������ꡡ1���ؿ��δ��ä����� 05�ܾ븩11 ����١�������(PDF)
�¤ϰ켡�ؿ��δ�������ʤΤǤ���������Τ�����������Ū�ǤϤʤ��Τǡ�
����Ψ���㤯�ʤäƤ��ޤ������פ�����Ǥ���
�ְ켡�ؿ��δ��ä�����פȤ��������ȥ�ˤ��Ƥ��ޤ��ޤ�������
�⤦����äȤ���̾��������褦�ʵ������Ƥ��ޤ���
�Ȥꤢ�����Ϥ���ǡ�
���ء���������ꡡ�켡�ؿ��δ��ä����� 05�ܾ븩11 ����١�������(PDF)
�������05�ܾ븩�����ء������������
05�ܾ븩�����ء����������
�ܾ븩���������������٤��⤤�Ǥ��͡�
��������ο������ʤ��褦�˴����ޤ�����
����Ǥϡ����ؤ��������̤ϤۤȤ�����������ʤ��Ǥ��礦��
�⤦����äȡ��������꤬¿���Ƥ⤤�����ʤ��Ȥ����������ޤ���
���ؤ����դ����̤ˤȤäƤϤ�꤬���Τ�������Ǥ��͡�
05��긩 ��������ꡡ������

���ء���������� 05��긩����������(PDF)
��긩�δ�������Ф����ץ��ȤǤ���
���ʽ��٥�Τ�ΤǤ��Τǡ����ؤ����ʿͤˤȤäƤϤȤäĤ��䤹���ץ��Ȥ��Ȼפ��ޤ���
�������꤬���äƤ���פȸ��������ǡ��⤦���Τ����ˤʤäƤ��ޤ����̤⤤�ޤ����顣
�դˡ��������꤬���äƤ���פȸ����ƶ�ʳ�������̤��Ƥ����ȻפäƤ���ΤǤ����͡�
���ء���������� 05��긩����������(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
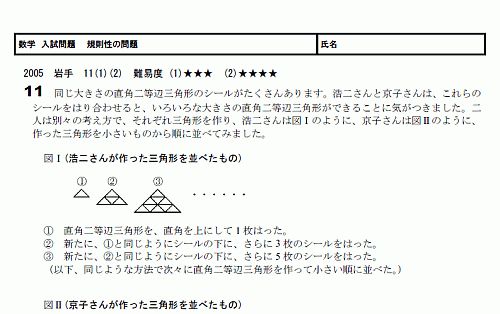
����� ��§��������
���ء���������ꡡ��§�������� 05��긩11 ����١�������(PDF)
�����ȿ����Ƥ��ФǤ���ΤǤ���������ʾ�Ǥ⤽��ʲ��Ǥ�ʤ��Ȥ�������
������ʤ�����Ȥ�������
�ʤ�Ȥʤ�������Ԥΰտޤ�ʬ����ޤ���Ǥ�����
�������ʤ�ۤɤͤ����Ȥ����Τ�����Ф褤�ΤǤ�����
���ء���������ꡡ��§�������� 05��긩11 ����١�������(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
��ʿ�������������ѡ�05���

���ء���������ꡡ��ʿ�������������� 05��긩10��(2) ����١�������(PDF)
���Ѥ���뤿��ˡ�ľ�ѻ��ѷ������Ѥ���ɬ�פ�Ĺ������Ƥ����ޤ���
�褤������Ȼפ��ޤ���
���ء���������ꡡ��ʿ�������������� 05��긩10��(2) ����١�������(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
����� ��ʿ��������������
����� ��ʿ��������������

���ء���������ꡡ��ʿ�������������� 05��긩10��(2) ����١�������(PDF)
���Ѥ���뤿��ˡ�ľ�ѻ��ѷ������Ѥ���ɬ�פ�Ĺ������Ƥ����ޤ���
�褤������Ȼפ��ޤ���
���ء���������ꡡ��ʿ�������������� 05��긩10��(2) ����١�������(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
����� 2���ؿ������ѿ�

���ء���������ꡡ2���ؿ������ѿ���05��긩8��(2) ����١�������(PDF)
���ѿ����Ѥ������������äƲޤ���
���ѿ������������Ǥ������̤��¤��Ƥ��ޤ���
��礬ʣ���ǡ�����Ĺ���ʤ꤬��������Ǥ��礦��
���ء���������ꡡ2���ؿ������ѿ���05��긩8��(2) ����١�������(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
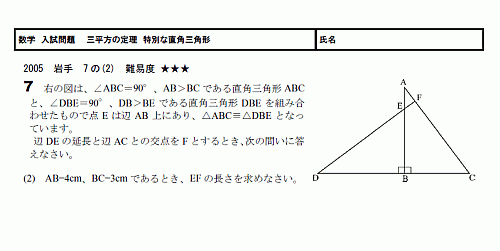
����� ��ʿ�������������̤�ľ�ѻ��ѷ�
���ء���������ꡡ��ʿ�������������̤�ľ�ѻ��ѷ���05��긩7��(2) ����١�����(PDF)
��������̤�ľ�ѻ��ѷ������Ȥ��ޤ���
���̤����̤�ľ�ѻ��ѷ��ϡ������구�λ��ѷ���ؤ��ޤ�����
�դ��椬�����������Ȥʤ�ľ�ѻ��ѷ��⡢���̤�ľ�ѻ��ѷ����ϰϤ�����ƹͤ��Ƥ��ޤ���
���ء���������ꡡ��ʿ�������������̤�ľ�ѻ��ѷ���05��긩7��(2) ����١�����(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
����� ϢΩ������������

���ء���������ꡡϢΩ������������ 05��긩5 ����١�����(PDF)
ϢΩ�����������Ѥ�����Ǥ���
����٤Ϥ���ۤɹ⤯����ޤ���
�����������ʽ�˺ܤäƤ���褦��������ϡ������ҤͤäƤ���ޤ���
�ʤ�Ȥʤ��������Ȥ߹�碌�����������äƤ����Ƥ��ޤ�����������ǤϤ���ޤ���
���ء���������ꡡϢΩ������������ 05��긩5 ����١�����(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
����� ����դ�����

���ء���������ꡡ����դ����� 05��긩4 ����١�����(PDF)
���֡���Υ��®��������Ǥ���
ʸ�����ɤ�����ǤϤ��ޤ�������Ǥ��ʤ�����Ǥ⡢
����դ���Ȥˤ�äơ��ºݤΰ�ư���ͻҤ��褯ʬ����褦�ˤʤ�ޤ���
��Ϻ����ʬ��ˤɤΰ��֤ˤ���Τ���®���ϤɤΤ��餤�ʤΤ�(ľ���η���)���ʤɡ�
����Ǥ�褯���ꤵ��ޤ���
���ʤߤˡ�(2)������٤ϡ��������Ǥ⤤���Ȼפ��ޤ���
���ͽ�Ū�ʤ�������ȡ�2ľ���μ�����Ƥ��顢�����κ�ɸ��Ф��פȤʤ�Ȼפ��ޤ��������ʤ�ȡ����ݤ������Τǥߥ��������ޤ���
������������٤�������Ȥ��Ƥ���Τϥ���դ�ºݤ˽Ƥߤ�ȴ�ñ�˵�ޤ뤫��Ǥ���
���ء���������ꡡ����դ����� 05��긩4 ����١�����(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
����� ����

���ء���������ꡡ���� 05��긩4 ����١�����(PDF)
���Ѥ�����Ǥ���
�����νΤǤϡ����٤��������(�������ȸ����褦�Ǥ���)�ϤȤƤ�����夬��ޤ�����
�ऺ�������������䤯�餤�¤٤��ץ��Ȥ��Ѱդ��ơ��ߤ�ʤ��Ϥ��ޤ���
�����ơ��ߤ�ʤǶ��褷�ޤ���
(���饹�οͿ��ϣ��ͤ��餤�Ǥ���)
���̤Ϥɤ����꤫��ĩ�路�Ƥ�褯��������顢�����ΤȤ����˻��äƹԤäơ�������碌�Ƥ��äơ����ɤ������ǧ���ޤ���
A�Ҥ������ܤ��Ǥ��������ΤȤ��������Ƥ���äƤ��Ƹ����ޤ���
�����������פȸ����ȡ�
�ۤ��λҤ������֤��������⤦���ۤ�Ȥˤ�������äƤ�Ρ��ס�
A�Ҥ��֤��äƤ�ˤ��ޤäƤ��
����ȡ�B�ˤ��֤ء����졢���֤�����Ǥ������ͤ�����
�ȸ��ä������ΤȤ��������Ƥ���äƤ����ޤ���
C�Ҥ��֤ͤ���������B�ˤ�������äƤ롩��
�����ֹ�äƤ롣��
C�ҡ֤����� ������� �衼�����������⽸�椷�Ƥ������
�ʤɤȤ������˿ʹԤ��Ƥ����ޤ���
���������Ȥˤ褯���봶���Ǥ���
���������Τϡ����Ϳ����饹�Ǥ�äƤ��������פμ��Ȥ��Ȼפ��ޤ���
�ҤȤ���ٶ����Ƥ��Ƥ�ʤ��ʤ���������������̣�廊�ޤ���
���٤��������ϡ������Ȥ������ʤ��ơ�������Ǥ�����Ӥ�̣�廊�ޤ���
���ؤ������ˤʤ�Ҥ�����������������Ȼפ��ޤ���
���ء���������ꡡ���� 05��긩4 ����١�����(PDF)
��긩��05ǯ�����������Ϥ�����Ǥ���
05 ��긩 ���������
�������꤬���Ū¿���褦�Ǥ���
���ֺǸ������ˤϰ��ä����äƤ��ޤ��ޤ�����
�����Τ����ˡ������ޤ���͡�
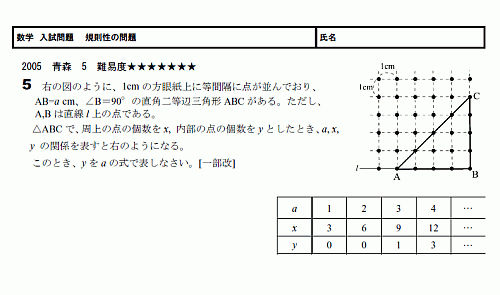
����� ��§��������
���ء���������ꡡ��§��������(ͶƳ������ӽ�) 05�Ŀ���5 ����١�������������(PDF)
����������������Ǥ������������ȤƤ�����
���ؤ����դ����̤Ǥ⤫�ʤ���֤�������ΤǤϤʤ��Ǥ��礦����
3���ֹͤ�����ͤ���ʬ�ˤ���ޤ���
�ºݤ�����ˤϡ�ͶƳŪ�פ˽��ꤵ��Ƥ��ޤ���
��ͶƳŪ�פȤ�����ˤ�����ޤǤιͤ�����
�����Ĥ��������ʬ���ƽ��ꤹ�뤳�ȤǤ���
�����ͶƳŪ�ˤ��뤳�Ȥˤ�äơ����䤹���ʤ�ޤ���
���ؤ����դ����̤ˤϤ��ҡ�ͶƳ������ӽ�������������������ĩ�路�Ƥߤ��ߤ����Ǥ���
���ء���������ꡡ��§��������(ͶƳ������ӽ�) 05�Ŀ���5 ����١�������������(PDF)
�ºݤˤϤ�������˽��ꤵ��Ƥ��ޤ���
���ء���������ꡡ��§�������� 05�Ŀ���5 ����١���������(PDF)
�Ŀ�����05ǯ�����������Ϥ�����Ǥ���
����� ��äȤ�û���ʤ�Ȥ�(�ؿ���)
����� ��äȤ�û���ʤ�Ȥ�(�ؿ���)
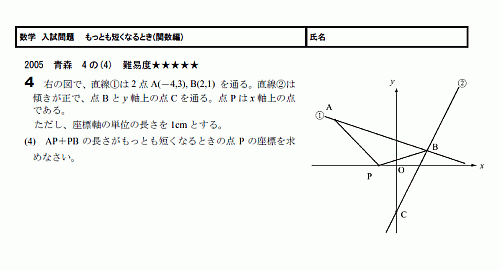
���ء���������ꡡ��äȤ�û���ʤ�Ȥ�(�ؿ���) 05�Ŀ���4��(4) ����١���������(PDF)
��������Ǥ褯�Ф�Τ��֤�äȤ�û���ʤ�Ȥ��פȤ�����
�ؿ��䡢����Ω�Τǽ��ꤵ��ޤ���
���ΡֺǤ�û���ʤ�Ȥ��פȤ�����郎�Ф��줿�Ȥ����פ��⤫�٤ʤ���Фʤ�ʤ�������ɤϡ�ľ���פǤ���
��Ĥ�����ľ���Ƿ����Ȥ����ֺǤ�û���ʤ�פΤǤ���
ľ���Ƿ�٤ʤ��Ȥ��ϡ�ľ���Ƿ�٤�褦�˹��פ��Ƥ����ޤ���
���ء���������ꡡ��äȤ�û���ʤ�Ȥ�(�ؿ���) 05�Ŀ���4��(4) ����١���������(PDF)
����� ľ���Υ���դȿ�
���ء���������ꡡľ���Υ���դȿ� 05�Ŀ���4��(3) ����١�������(PDF)
��������Ȼפ��ޤ���
����äȤ����Ҥ���ɬ�פȤ��ޤ���
������ɤϡֹ�Ʊ�ʿ��ס�
�ֻ�ʿ���������פ�ȤäƤ�Ǥ��ޤ���������äȷ���ʣ���ˤʤ�ޤ���
���ء���������ꡡľ���Υ���դȿ� 05�Ŀ���4��(3) ����١�������(PDF)
����� ������
���ء���������ꡡ����ξ��� 05�Ŀ���3��(2) ����١�����(PDF)
����ξ��������ꡣ
����Ϣ�����������Ѥ��ޤ���
����٤�3�ˤ��Ƥ��ޤ�����2�Ǥ⤤�����⤷��ޤ���
����äȶä������ȡ�
������Ҥο��ؤζ��ʽ�ϡ����ѷ���������Τ�����?��?��Ȥä������������˾ä��Ƥ��ޤ��͡�
?3�Ȥ��դ��椬��������
?2�Ȥ��դ��椬�����������δ֤γѤ���������
�ˤĤʤ���������㤬�����ʤ��ΤǤ���
���Ȼ��֤����ʤ��Τǡ����礦���ʤ��Τ��⤷��ޤ���
����äȼ䤷���褦�ʵ������ޤ��͡�
���ء���������ꡡ����ξ��� 05�Ŀ���3��(2) ����١�����(PDF)
����� ��ʿ����������������
���ء���������ꡡ��ʿ����������������
���ء���������ꡡ��ʿ���������������� 05�Ŀ���3��(1) ����١�����(PDF)
��ʿ��������������Ǥ���
���ʽ�ˤ���褦�ʴ�������ǤϤʤ�������äȹ��פ�ɬ�פ�����Ǥ������פ���������Ȥ��Τǡ��Ȥꤢ�����ֻ�ʿ�����������������פȤ����������ǤҤȤ�����ˤ������Ȼפ��ޤ���
���ޤꡢ̾�����褯����ޤ���
���ء���������ꡡ��ʿ���������������� 05�Ŀ���3��(1) ����١�����(PDF)
������Ψ

���ء���������ꡡ��Ψ 05�Ŀ���2��(2) ����١�����(PDF)
���γ�Ψ������ϡ����ʽ�ˤ�Ʊ���褦�ʤ�νФƤ��ʤ��Τǡ������Ϥ����ޤ���
�����ޤ����ä���������вޤ���
���ء���������ꡡ��Ψ 05�Ŀ���2��(2) ����١�����(PDF)
05�Ŀ��������ء����������
�Ŀ�������������ϡ������꤬�����Ĥ��Фޤ��͡�
4��5�����꤬���Ȼפ��ޤ���
����������������¿�����ꤵ��Ƥ���Τǡ����ʽ��٥�����꤬���ä����С�70������ϼ���Ȼפ��ޤ���
05�̳�ƻ ��������ꡡ������

���ء���������ꡡ�����ԡ�05�̳�ƻ(PDF)
���������δ���Ū�������ƥץ��Ȥˤ��ޤ�����
2005ǯ���̳�ƻ�ι��������Ǥ���
���ؤ��������̤���������ΤˤϤ��礦�ɤ褤�ץ��ȤǤ���
�Ǥ��ʤ��ä����꤬���ä��顢�⤦���ٶ��ʽ�ˤ�ɤäƳ�ǧ������Ϥ��Ĥ��Ƥ����ޤ�������������ǫ�˴�ĥ������
���ؤ������η������Ȥ������Ѥ���Τ�褤�Ȼפ��ޤ���
���ء���������ꡡ�����ԡ�05�̳�ƻ(PDF)
����� ��ʿ�������� ����

���ء��������ꡡ05 �̳�ƻ 5��(2)������١���������ʿ�������� ����(PDF)
��ʿ�������������Ѥ��ơ�ɬ�פ��դ�Ĺ�����ᡢ
������Ȥä����Ѥ���ޤ���
ɸ��Ū������Ǥ���
���ء��������ꡡ05 �̳�ƻ 5��(2)������١���������ʿ�������� ����(PDF)
����� ư��������

���ء��������ꡡ05 �̳�ƻ 5��(2)������١���������ư�������ꡡ������(PDF)
ư��������Ǥ���
����ư������Τ��Ȥ�ư��������Ƥ֤��Ȥˤ��ޤ���
��������������¿�����ꤵ��ޤ���
�ؿ����������������Ϥ��������꤬¿���Ǥ���
ư�������꤬ʬ����褦�ˤʤ�С����ؤ�����������Ȼפ��ޤ���
���Ҵ�ĥ�äƤ���������
��������ϡ�PQ//AB�Ȥ�������Ĥ��äƤ��ޤ��������ˤǤ���С�
���Ȥ��Ǥ���Ȼפ��ޤ���
���ء��������ꡡ05 �̳�ƻ 5��(2)������١���������ư�������ꡡ������(PDF)
����� ��ʿ�������������̤�ľ�ѻ��ѷ�

���ء��������ꡡ05 �̳�ƻ 4��(3)������١���������ʿ�������������̤�ľ�ѻ��ѷ�(PDF)
��ʿ���������������ջ��ѷ������������Ѥ�������Ǥ���
����٤ϣ��ȤʤäƤ��ޤ��������Ǥ⤤�����⤷��ޤ���
�����������ƹͤ��ʤ���Фʤ�ʤ��Τǡ�
�����ǤϤ����ʤ��Ȥ������Ȥǣ��ˤ��ޤ�����
���ء��������ꡡ05 �̳�ƻ 4��(3)������١���������ʿ�������������̤�ľ�ѻ��ѷ�(PDF)
����������
���ء��������ꡡ05 �̳�ƻ 4��(1)������١����������Ⱦ��������(PDF)
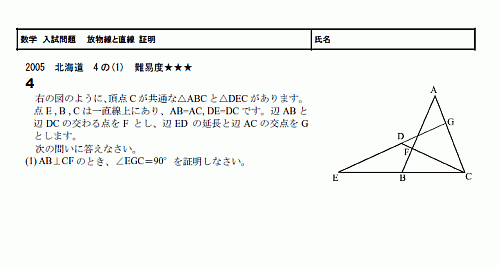
���ξ���������Ǥ���
�����ϡ�����פ����Ѥ��Ƥ��ơ����ƥ���������פ�ʬ�ष�Ƥ��ޤ�������������Ѥ��ʤ��Ƥ�����Ǥ��ޤ���
�����ջ��ѷ������������Ѥ��ơ�������ʤ�Ƥ����ޤ���
���ء��������ꡡ05 �̳�ƻ 4��(1)������١����������Ⱦ��������(PDF)
����� ��ʪ����ľ������ʬ����

���ء��������ꡡ05 �̳�ƻ 3��(2)������١���������ʪ����ľ������ʬ����(PDF)
����ˤ褯���ꤵ��륿���פ�����Ǥ���
�Ǹ��������Ȥ��������μ���������ħ�Ǥ��礦��
���ء��������ꡡ05 �̳�ƻ 3��(2)������١���������ʪ����ľ������ʬ����(PDF)
����� ��������������(ʸ����)

���ء��������ꡡ��������������(ʸ����)(PDF)
���������ˤϤ��ʤ��ߤΡ����Ѥ˴ؤ�������Ǥ���
������Υ��Ĥ����Ф���С����ۤ�������ޤ���͡�
���ء��������ꡡ��������������(ʸ����)(PDF)
����� ϢΩ������������(ʸ����)

���ء��������ꡡϢΩ������������(ʸ����)(PDF)
05 �̳�ƻ 2��(1)������١�����
���Ū�䤵����ʸ������Ȼפ��ޤ���
��Ω�����������Ǥϡ�����ۤ���ʸ����Ͻ��ꤵ��ޤ���
���Τ��餤�Υ�٥���������ǫ�˲��Ϥ��Ĥ��Ƥ����ޤ���
���ء��������ꡡϢΩ������������(ʸ����)(PDF)
����� ʿ����
05 �̳�ƻ 1��7������١�����
ʿ�������μ���������вޤ�������ʿ�����������μ�������ȡ���äȥ��ࡼ���˲�Ȼפ��ޤ���
����٤������ϡ֡��פǤ⤤���Ȼפ��ޤ���
�����ơ֡������פˤ����Τϡ��������Ф��ꤷ�ƤǤ���ȻפäƤ��뤻���Ȥϡ������������꤬�Ǥ��ʤ������ˤ��뤫��Ǥ������֤��ơ����ä���ͤ����ߤ����Ȼפ��ޤ���
ʬ���ä��Ȥ��Ϥ��줷���Ǥ��衣
��ʿ��������������1
˿������������ꡣ
�����ǤϤ����ʤ��Ȥ��������Ǥ���
����1
���Ѥ�����Ǥ���
�����ջ��ѷ������������Ѥ��ʤ���Фʤ�ʤ�ʬ�����ʤäƤ��ޤ���
��Ψ
��ؿ��ؤγ�Ψ������Ǥ���
�����˽��ꤵ��Ƥ�����ΤǤ���
��Ψ������ϡ�ʣ��������ˤʤäƤ���ȡ��ޤ��������ꤹ��Τ˼�֤�������ޤ���
���μ�֤��ˤ��ޤ��ˤ�����ȡ�����Ǥ��ޤ���
����®���ˤλҤϡ���Ψ�����꤬���ʤΤǤϤʤ��Ǥ��礦����
������2
�������2���ܤǤ���
������ϡ�����ΰ��ֺǸ�˽Ф���륱������¿���Ǥ���
�ֲ���������ΤĤ������ס��Ȥ��ä������ǽФ���ޤ���
���������Ϲ�Ʊ�ξ������դ��ä����ǽФ���Ƥ��ޤ���
������1
���������Ǥϡ��������������꤬�Ҥ�Ѥ�˽��ꤵ��ޤ���
���������ع��ǤϤ��ä���������ʤ��褦�ǡ����λ����ˤʤ�����̤����䤷����ޤ���
��������Ƥ��ȡ�����Ǥ������̤�ɬ���Ȥ��äƤ����ۤɸ����ޤ���
�֤���Ȼ��������פ�����Ϥ���ޤ���?�פȡ�
���ε������Ϥ褯ʬ����ޤ���
Ʊ��������������Ƥ⡢�ּ�ʬ���Ǥ���褦�ˤʤäƤ��뤫�ɤ����פϳΤ�����ʤ���Ǥ���͡�
�����ơ����̤Τ���ˤ�����ʶ�������ĥ��Ф���õ���Ƥߤ�ΤǤ�����
�ʤ��ʤ����Ĥ���ޤ������֤������äơ�
���δ֡����̤��Ԥ����Ƥ���Τ����ޡ��ȤǤϤ���ޤ���
���Ȥ��������ʤ��ȻפäƤ��ޤ���
�����˰פ������꤫��������ޤǤ���ФǤ���褦���Ȥ����ΤǤ����͡�
���Τ���˾�����������Υǡ����١������äƹԤ������Ȼפ��ޤ���
�Ϥ�Ĥ������� ���ء���§����ͤ�������3
��§��������Ͽ͵����⤤�褦�Ǥ���
��§��������������������̤⤤�ޤ�����͡�
����Ϥ���äȤ䤵����Ǥ���
ɽ��ƹͤ����ʬ����䤹�����⤷��ޤ���
�Ϥ�Ĥ������� ���ء���§����ͤ�������3
�Ϥ�Ĥ������ꡡ�ߤ����1
�Ϥ�Ĥ������ꥷ�����
����ϡ���Ω��ؤ�����ƥ��Ȥǽ��ꤵ��Ƥ�������Ǥ���
�ʤ�Ȥʤ������Ǥ������¤Ϥ���ۤ�������ޤ���
(4)����������Ȼפ��ޤ���ʬ�������̤������50�ͤˤҤȤ꤯�餤�ǤϤʤ��Ǥ��礦����
�Ϥ�Ĥ������ꡡ��§����ͤ�������2
�Ϥ�Ĥ������ꡢ����§��������Ǥ���
���٤Ƥε�§��ȯ�����Ƥ�����Ȥ���ȡ��Ƥ�����ޤ���
��§�����Ĥ���Ȥ���������ˤʤäƤ��ޤ���
�������������ܤ��Ƥߤ�ȡ���ñ�˲ޤ���
�Ϥ�Ĥ������� ���ء���§����ͤ�������2
�Ϥ�Ĥ������ꡡ��§����ͤ�������1
���ؤ��������ˤϡ֤�������פȡְ�������פ�����ޤ���
���ؤ�ؤ֤Τϳڤ�����ΤǤ������꤬���Ȥ��Ϥ��줷�����ȴ����ޤ���
�ʤ��ˤϡ������䤿���ʣ�����ä��ꡢ�ͤ�����ʣ�����ä��ꤷ�ơ�
���Ȥ��Ƥ⤢�ޤꤦ�줷�����ʤ����꤬����ޤ���
�������������Ƥ�ڤ����ʤ�ޤ���
�դˡ����Ϥ�ͤ�����ñ��ǡ��֤ʤ�ۤɡ��פȻפ��������¸�ߤ����Τ�
�Ƥ��Ƴڤ����ʤ�ޤ���
�䤬���ޤǿ���Ƥ���������椫�顢����Ϥ���������ʡ��Ȼפä���Τ�ԥå����åפ��ƤޤȤ�Ƥ����ޤ���
�ǽ�ϵ�§��������Ǥ���
��§����ͤ�������ϡ����ؤ���Ǥ��äˤ��⤷������ΤΤҤȤĤ��Ȼפ��ޤ���
��������Ϥ䤵��������Ȥ�����Ǥ��礦����
->�Ϥ�Ĥ������� ���ء���§����ͤ�������1
���ء�������к��ץ���
�����ؤ����ʿͤ�
��أ�ǯ���ǡ����ؤ��������̤Τ���˺��������ץ��ȤǤ�����Ū�ϡ������Ǥο��ؤ�������夲�뤳�ȤǤ���
��أ�ǯ���Ρ�����ƥ����к��פȤ��Ƥ����ѤǤ��ޤ���







