立体の表面積
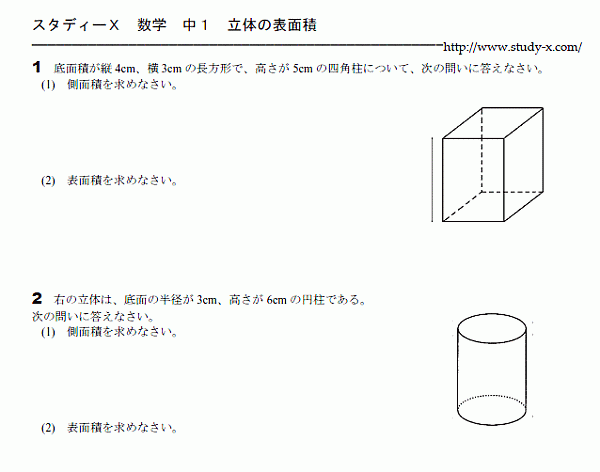
立体の表面積を求める問題です。
円錐の表面積は苦手とする生徒も多いです。
空間図形
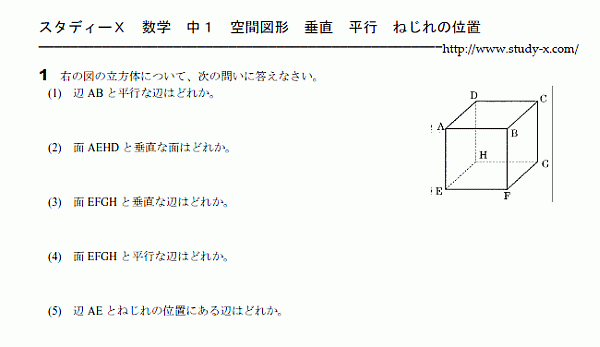
垂直、平行、ねじれの位置についての問題と
面積や長さを求める問題です。
扇形の中心角
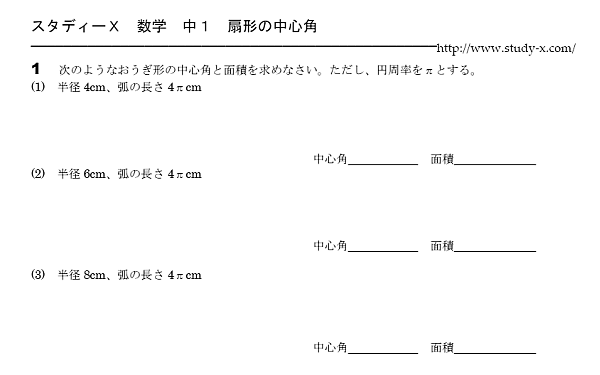
扇形の中心角を求める問題です。
扇形の面積が分かっているときは、
円の面積と扇形の面積を比べて、扇形が何倍になっているのかを調べます。
扇形の弧の長さが分かっているときは、
円の周の長さと扇形の弧の長さを比べて、扇形が何倍になっているのかを調べます。
扇形の割合が分かったら、中心角を求めていきます。
扇形の弧の長さと面積

扇形の弧の長さと面積を求める問題です。
まずは、中心角から、扇形が円に対してどのくらいの割合なのか(何倍なのか)を求める事が大事です。
公式を覚えて当てはめるだけの練習だと、あとあと意味側からなくて苦労します。
平面図形 作図 2

作図の問題その2です。(その1はこちら)
その1よりも少し難しい問題を入れてあります。
平面図形 作図 1
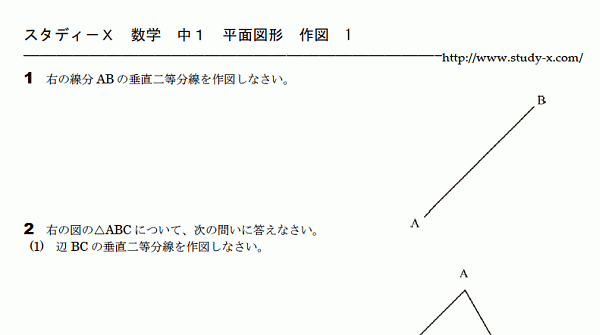
作図の問題です。
コンパスは距離を記憶する道具です。
1点からの距離が等しい点をたくさん集めると円になります。
2点からの距離が等しい点をたくさん集めると、2点を結ぶ線分の垂直二等分線となります。
2直線からの距離が等しい点をたくさん集めると、2直線が作る角の二等分線となります。
このことをしっかりイメージして作図していきましょう。
線対称と点対称
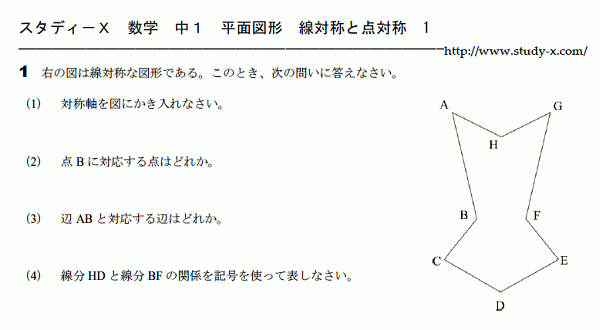
線対称と点対称のプリントです。
折ったときにぴったり重なる図形が線対称。
折り目を対称軸、または対称の軸といいます。
180度回転させたときにぴったり重なる図形が点対称です。
回転の中心となる点を対称の中心といいます。
図形が苦手な人へ。
ぜひ、実際に折ったり、回転させたりして確かめてください。
何度かやってみたら頭の中で折ったり回転させたりしてみることです。
繰り返すうちに、イメージできるようになってきます。
平面図形 基本
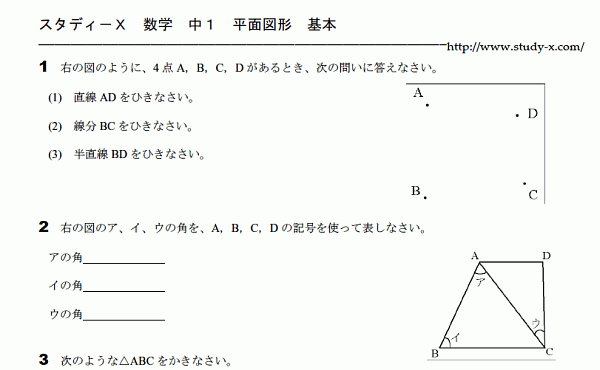
お待たせいたしました。
リクエストの多かった、平面図形のプリントです。
最初は基本問題となります。
とくに、角の表し方をしっかり覚えていなくて、
わけがわからなくなる生徒が結構いますので、
注意して覚えてください。
用語をしっかり頭に入れておかないと、
解説の意味がわからなくなってしまいます。
比例と反比例 比例と反比例の利用

比例と反比例の利用のプリントです。
応用問題ということができると思います。
苦手な生徒が多くなります。
コツは、型に当てはめて解こうとするのではなく、
文章の状況をちゃんと想像して、
表をかいてみて考えることです。
そうすると、比例の関係なのか、
反比例の関係なのかが見えてきます。
この作業を繰り返して初めて、
すらすら解けるようになります。
3の(2)の問題は難問です。
表をかいて考えてみよう。
比例と反比例 反比例の式とグラフ

反比例の式とグラフのプリントです。
グラフは、まず表をかきます。
xとyがともに整数となる点をとり、
双曲線をかきます。
比例と反比例 反比例

反比例の基本のプリントです。
xとyの値をかけると一定になる、
というのがイメージをつかみやすいと思います。
式に書くときは一般に y=a/x となります。
比例と反比例 比例のグラフ
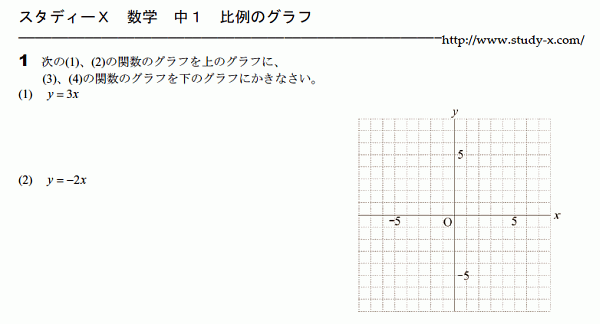
比例のグラフのプリントです。
簡単にかく方法もありますが、
最初のうちはまず表をかいて、
表をもとにしてグラフかくのが良いと思います。
そのうちに慣れてくると、
簡単なかき方を自分で法則化することができます。
比例と反比例 座標
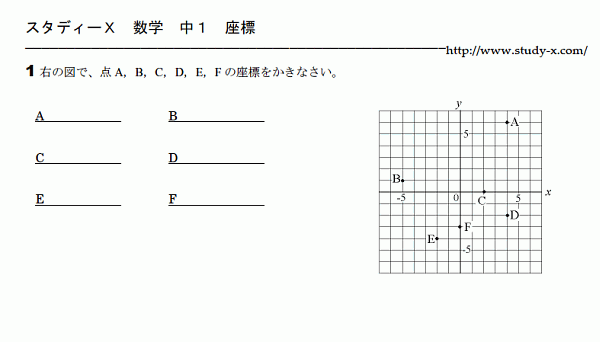
座標はしくみが分かれば非常にやさしいところです。
反対にここがしっかり分かっていないと、
あとでグラフをかくときに非常に苦労します。
比例が苦手で・・・という生徒が
座標のしくみがよく分かっていなかったということが
何度もありました。
(x座標,y座標)の順に並んでいることを
しっかり覚えて欲しいと思います。
比例と反比例 比例の式 変域

変域と比例の式を求める問題です。
1の変域の問題は、答え方が分からないかもしれません。
その意味でちょっと分かりづらい問題です。
でもぜひ意味を言えるようになって欲しいのです。
3のタイプの問題は、
私は「暗算で出せるものは積極的に暗算で出しなさい」と指導しています。
そのほうが比例の関係をつかみやすいし、
体になじませることができます。
代入して解くやり方も大事です。
しかし、安易にパターン化して覚えさせると、
比例の意味を考えなくなってしまいます。
それは避けなければなりません。
比例と反比例 比例の基本2

比例の基本のプリントです。
この手の問題は非常によく出題されます。
文字の式のつくり方がわかっていれば大丈夫です。
比例するかどうか判断がつかない場合は、表をかいてみることをお勧めします。
x=1のときの計算、x=2のときの計算がすべて同じ形になるということを理解できます。
また表をかくことで、xが2倍、3倍になるとyが2倍、3倍になるかを確かめることも出来ます。
比例と反比例 比例の基本1

比例の基本のプリントです。
・ xの値を2倍、3倍・・・にするとそれにともなってyの値も2倍、3倍になる。
・ y=ax
(yはxに決まった数をかけて求めることが出来る)
・ aを比例定数という。
・ yがxに比例するとき、比例定数はy÷xで求めることが出来る。
・ x=1のときのyの値が比例定数である。
一方の値と他方の値の対応関係をしっかりつかみたいところです。
方程式 方程式の利用1(文章題)

方程式の利用です。
この単元は苦手な子が多いです。
計算は良くても文章題になるとさっぱり分かりません。
多くの場合、そんな生徒はパターンを暗記して対応します。
計算のしくみが分かっていれば、暗記する必要はありません。
アドバイスとしては
「絵を描け」
「表をかけ」
です。
これは文章題を分かりやすくするための手段です。
方程式 分数を含む方程式2
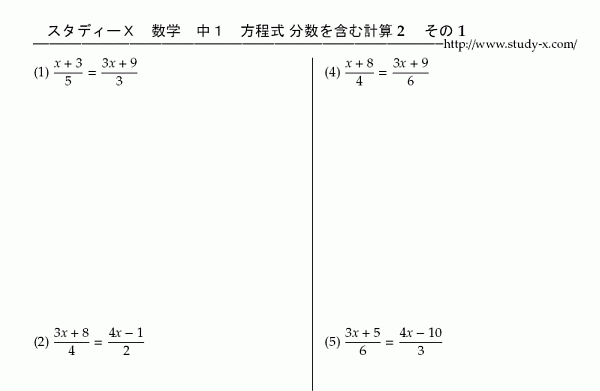
方程式の計算練習シリーズです。
分数をふくむ方程式の続き。
分子に複数の項があるタイプの問題です。
方程式の計算練習 分数をふくむ方程式2 その1〜その10(PDF)
方程式の計算練習 分数をふくむ方程式

方程式の計算練習シリーズです。
今回は分数をふくむ方程式です。
そのままでも計算できますが、分母をはらって計算すると、ミスを防ぐことができます。
方程式の計算練習 分数をふくむ方程式 その1〜その10(PDF)
方程式の計算練習 小数をふくむ方程式

方程式の計算練習シリーズです。
今回は小数をふくむ方程式です。
そのままでも計算できますが、両辺を10倍、100倍してから計算するとミスが少なくなります。
方程式の計算練習 小数をふくむ方程式 その1〜その10(PDF)
方程式の計算練習 かっこをふくむ方程式

方程式の計算練習シリーズです。
今回はかっこをふくむ方程式です。
この方程式がすばやく正確に解けるようになれば、
マスターしたといえるまであと一歩です。
(あとは、小数と分数の計算と、文章題。)
方程式の計算練習 かっこをふくむ方程式 その1〜その10(PDF)
方程式の計算練習 移項(項が4つのタイプ)

方程式の計算練習シリーズです。
移項の練習です。
項が4つのタイプのものを10枚作成しました。
xの項を左辺に、数字だけの項(定数項)を右辺に移項します。
方程式の計算練習 移項(項が4つのタイプ) その1〜その10(PDF)
方程式の計算練習 移項(項が3つのタイプ)
方程式の計算練習 移項(項が3つのタイプ)

方程式の計算練習シリーズ。
移項の練習です。
項が3つのタイプのものを10枚作成しました。
xの項を左辺に、数字だけの項(定数項)を右辺に移項します。
方程式の計算練習 移項(項が3つのタイプ) その1〜その10(PDF)
方程式の計算練習 基本3、4タイプ

方程式の計算練習の基本3、4タイプを集めたものです。
A=BならばA×C=B×C
A=BならばA÷C=B÷C
の問題です。
あまり速さばかり追うと意味を考えなくなってしまいますので注意が必要です。
意味が分かって解けているという状態が望ましいです。
特に、
2x=10
と
x/2=10
の違いがよく分かっていない生徒は結構います。
x=5? それともx=20?
どっちがどっち?
と混乱している生徒は意味が分かっていません。
2x=10
はxを2倍したら10になるという意味。
x/2=10
はxを2で割ったら10になるという意味です。
意味を考えれば、xを求めるのはとても簡単です。
方程式の計算練習 基本3、4タイプ その1〜その10(PDF)
方程式の計算練習 基本1、2タイプ

方程式の計算練習の基本2タイプを集めたものです。
A=BならばA+C=B+C
A=BならばA-C=B-C
を利用した問題10ページです。
家庭などでの反復学習用に量を多くしました。
方程式の計算練習 基本1、2タイプ その1〜その10(PDF)
方程式の計算練習 基本4タイプ

方程式の計算練習の基本4タイプを集めたものです。
A=BならばA+C=B+C
A=BならばA-C=B-C
A=BならばA×C=B×C
A=BならばA÷C=B÷C
を考えながら練習したいところです。
正負の数その1 中1

正負の数の授業用プリントです。
この単元では
正の数と負の数は、
・反対の意味を表すこと
・基準が存在すること
をはっきり意識させていきたいです。
中1 数学 文字の式 関係を表す式(公式)
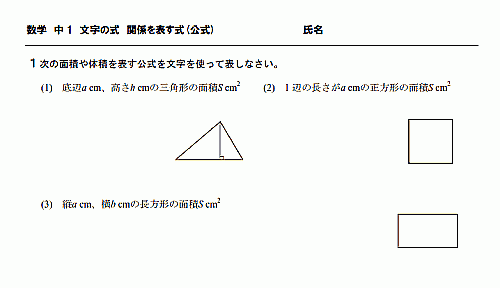
関係を表す式の公式編です。
公式は文字で表すと、言葉で表すよりずっと簡単になります。
文字の式の恩恵を受けているわけです。
中1 数学 文字の式 関係を表す式

数量の関係を等式に表します。
文字の式の導入から少し発展した形。
ここが苦手な生徒は、結構います。
「文字のところに数字を当てはめて考えてみればいいよ。」
と教えると、とたんにできるようになる生徒もいます。
つまり、「a円のりんごを5個買ったらb円だった」
というもんだいのaのところに100円、bのところに500円を入れて
式を考えてみるのです。
100×5=500
という式が出ます。
この式をもとに、文字を入れなおします。
100のところにa,500のところにb の文字を入れてできあがり、というわけ。
「文字のところに数字を当てはめて考えてみる」というヒントで
分からない生徒は、この先、方程式の文章題が苦手になる可能性が高いです。
そんな子は、小学校のときも文章題が苦手だったのではないでしょうか。
算数の授業ではあまり考えずに、先生が書いた黒板の式のまねをして式を書いていたタイプです。それでなんとなく正解できてしまう。そして、自分はできるようになったと思い込んでしまう。こんな生徒はたくさんいます。
「まねするだけ」の算数から早く抜け出す必要があります。
お勧めは、小学校のときの文章題を絵を描きながら一問ずつやってみるというやり方です。時間はかかりますが、このさきなんとなく方程式を解くというのよりはずっといいと思いますよ。
中1 数学 文字の式 分配法則2

文字の式のうち、分配法則を使ったものです。
手順としては、分配法則を使ってかっこをはずし、
それから同類項をまとめます。
※07.09.10
答えの間違いを修正しました。
ご指摘ありがとうございました。
解答 1(7)
誤)5x+36 → 正)5x+31
中1 数学 文字の式 分配法則

文字の式のうち、分配法則を使ったものです。
分数のものは教科書で少ししか扱われていないせいか、毎年苦手な生徒が若干名出る気がします。
中1 数学 文字の式のかけ算 わり算

文字の式のかけ算、わり算です。
プラスマイナスの符号に注意して計算します。
ここでつまづく子供はほとんどいません。
かけ算、わり算ができないか、
またはかけ算、わり算のプラスマイナスの法則を覚えていないか、のどちらかだと思われます。
中1 数学 式を簡単にする かっこあり

ここが文字の式の最も重要なところと言っていいと思います。
式を簡単にする問題のうち、かっこのあるものです。
プラスマイナスの符号に注意します。
中1 数学 式を簡単にする 一次式の加法、減法

ここが文字の式の最も重要なところと言っていいと思います。
数学が苦手な中学3年生を教えたことがありますが、ここの単元ができていないことが苦手の原因だったことがありました。
その生徒はここが分かったら、方程式や連立方程式などの計算問題の正答率がぐーんと上がりました。
このプリントが良く分からない生徒の多くは、
正負の数の計算が分かっていないか、
項と係数の理解ができていないか、のどちらかです。
そのページに戻って理解しましょう。
ここの単元のプリントは特に充実させたいと思っています。
中1 数学 項と係数

項と係数という言葉の意味が分かっているか確かめます。
文字の式が苦手な中学生は、「項」が理解できていないことが多いです。
単純に言うと、「どこで切れるのか」ということ。
あるいは「どこがまとまりなのか」ということです。
4x−3y+5という式なら
4x と −3y と 5に分けることができ、
そのそれぞれを項とい言います。
これから数学を学んでいく上で大事な言葉ですので、しっかり理解しましょう。
中1 数学 式の値 累乗
式の値を求める問題のうち、累乗のプリントです。
分数と同じく、累乗でも注意が必要です。
ここでつまづく生徒は、累乗の計算が良く分かっていないケースが多いので、中1 数学 正負の数 累乗・指数に戻ってしっかり理解して練習しておくとよいでしょう。
中1 数学 式の値 分数
式の値を求める問題では、分数になるとつまづいてしまう生徒が多いものです。
ここで、分数と割り算の意味の関係をしっかりと押さえておきたいです。
できれば、もう少しプリントを追加したいと思います。
中1 数学 式の値
文字の式のうち、式の値を求める練習プリントです。
数学の中でも特に大事な「代入」を練習します。
ポイントはマイナスの値を代入するとき。
符号に注意が必要です。
中1 数学 文字の式の表し方2
文字の式の表し方のうち、複雑なものです。
+、−の記号は省きませんので、注意が必要です。
中1 数学 数量を表す式
このプリントでは、文字の式の表し方の決まりに従って、数量を表す練習をします。
さらにいい状態は、できた式を見て、その式がいったい何を表しているのかが分かることです。そうなれば、この先習う単元のの方程式の文章題が得意になります。
中1 数学 文字の式の表し方
文字の式の表し方を学習するプリントです。
文字の式はふつう×、÷の記号を省いて表します。
その他、文字の式の表し方の決まりにしたがって式を表す練習をしましょう。
中1 数学 文字の式
文字の式とは何かを学習するプリントです。
文字の式を使うと、計算や数の関係をとても簡単に表すことができます。
まずは、文字を使ってどんな風に式を表すかを練習してみましょう。
中1 数学 正負の数 四則混合計算
たし算、ひき算、かけ算、わり算、累乗、かっこが組み合わさった計算です。
この計算がすらすらできれば、正負の数は理解できたと言って良いでしょう。
中1 数学 正負の数 乗法・除法 3つ以上の計算(2)
正負の数 かけ算・わり算が3つ以上ある計算のプリントの2回目です。
中1 数学 正負の数 累乗・指数
指数でつまづく生徒はとても多いです。
よく考えると、確かにややこしい。
指数がどこについているのかに注目する必要があります。
たとえば2乗するときの例。
指数が数字についてるときは、絶対値だけ2乗します。
指数がとじかっこについているときは、かっこ全体を2乗します。
中1 数学 正負の数 乗法・除法 符号判断
正負の数の掛け算・割り算のプリントで、最も基本的なものです。
−7×5 などのような問題です。
符号を正しくつけることができればOKです。
中1 数学 正負の数 乗法・除法 3つ以上の計算
3つ以上のかけ算、わり算です。
1 わり算をかけ算になおす、
2 約分する
という流れで計算します。
中1 数学 正負の数 乗法・除法 逆数
正負の数の乗法(かけ算)・除法(わり算)のプリントです。
わり算が混じっているときは、逆数にしてかけ算に直すと、式全体をすっきりさせることが出来て、計算が簡単になります。
中1 数学 正負の数 項が3つ以上の計算2
項が3つ以上の計算のプリント2枚目です。
もうちょっと増やしたいと思っています。
まずは、自分のためにも、中学数学の全体のプリントを作成したいと思っています。
中1 数学 正負の数 項が3つ以上の計算1
項が3つ以上の計算です。
簡単に計算するには、正の項どうし、負の項どうしでまとめることです。
簡単な計算方法をとると、ミスも少なくなります。
中1 数学 正負の数の計算2
正負の数の計算のうち、負の数を足したり引いたりする問題です。
かっこをはずして考える問題と捉えてもいいです。
中1 数学 正負の数の計算
数直線で考えるタイプの問題です。
正負の数の計算はぜひともマスターさせておきたいところです。
ここで躓くと、このあとの数学が出来なくなってしまいます。
もう少し、問題数を増やす予定です。
しばらくお待ちください。
中1 数学 正負の数の大小
正負の数の大小を比べる問題です。
数直線を描いて考えることができると、かんたんです。
そのうち、数直線を描かなくても頭の中にイメージできるようになります。
そうなれば、しめたものです。
中1 数学 正負の数 1の3
中学1年で習う、正負の数のプリントです。
プラスの数とマイナスの数はちょうど反対のことを表します。
前半はそのことのまとめです。
国語力も要求されると思います。
後半は絶対値。
「絶対値は、プラスとマイナスの符号をとったもの」と理解している生徒がいますが、
それでは不十分です。絶対値とは0からの距離を表します。
問題を解くたびに数直線をを書いて考えると、絶対値をよく理解できます。
中1 数学 正負の数 1の2
正負の数を理解するプリントです。
正の数と負の数を「ちょうど反対の概念」として理解するためのプリントです。
実を言うと、この辺は分からなくても先に進めます。
特に今後の学習に差支えがないといってもよいと思います。
しかし、それでも生徒にこの辺のことを理解してもらい、
「なるほどマイナスの数って便利だなあ。」と感じてもらえると、
のちのちの数学が楽しくなるのではないかとも思います。
中1 数学 正負の数 1の1
中1の数学
正負の数の学習プリントです。
正負の数の最も基本的な問題を扱っています。
[目標]
・それぞれの数の大小が分かる。
・マイナスの数とは何なのかが分かる。
※解答はまだです。お待ちください。



